例题1

一人爬有20个阶梯的楼梯，假定每次向上爬5个阶梯，又下走3个阶梯，问该人需几次能跑到楼梯顶部？

A.7

B.8

C.9

D.10

解法：

该人需要（20-3）÷（5-3）=9（次），即9次能跑到楼梯顶部。

因此，选择C选项。

知识点：

过河问题：假如有N个人过河，船最多载M个人，则过河次数为（N-1）/（M-1）（过河时间指单程时间）。此公式适用条件是，题目中没有明显说明划船人数，默认为1个人，分子和分母同时减1,可以把这一个人当成固定划船人。

假如有N个人要过河，船上能载M个人，而需要a个人划船。那么从N个人中找出a个人当船夫，这样就变成了（N-a）个人要过河，而船上除了船夫以外一次只能载（M-a）个人，次数显然就是（N-a）/（M-a）次。

例题2

某地有耕地20万亩，其中75%用于种植粮食，其余用于种植经济作物。当地居民生活需要消耗10万亩的粮食，其余用于出售，粮食每亩年收入1000元，经济作物每亩年收入5000元。当地政府正在积极推进退耕还林政策，每亩退耕还林的耕地可享受500元/年的财政补贴。不考虑其他因素，为使居民收入实现每年10%以上增长，且保证粮食种植面积不低于12万亩，2年内至多可以有（）亩耕地进行退耕还林。

A.10000

B.12666

C.13333

D.15000

解法：

根据“20万亩的75%用于种植粮食”，可知：20×75%=15万亩种植粮食。

根据“生活需要消耗10万亩的粮食，其余用于出售”，可知：退耕还林前，该地10万亩粮食用于生活消耗，15-10=5万亩粮食用于出售，20-15=5万亩种植经济作物。

根据“粮食每亩年收入1000元，经济作物每亩年收入5000元”，可知：该地年收入1000×5＋5000×5=30000（万元）。

根据“每亩退耕还林的耕地可享受500元/年的财政补贴”，可知：退耕还林的补贴低于种植粮食的收入。为使居民收入实现每年10%以上增长，需保障12万亩粮食种植面积，原种植粮食的3万亩耕地，一部分退耕还林、一部分改种植经济作物。

设2年内有x万亩耕地进行退耕还林，则有

解得x≦3.8/3≈1.2666（万亩），即1.2666万亩=12666亩。

因此，选择B选项。

例题3

某部门正在准备会议材料，共有153份相同的文件，需要装到大小两种文件袋里送至会场，大的每个能装24份文件，小的每个能装15份文件。如果要使每个文件袋都正好装满，则需要大文件袋（）个。

A.2

B.3

C.5

D.7

解法：

设需要大文件袋x个，小文件袋y个。

根据“共有153份相同的文件”，可列方程：24x+15y=153，化简得8x+5y=51。

依次代入选项验证：

因此，选择A选项。

例题4

某商店以每件6元的进价买回一批商品，售价为每件8.4元，当卖了这批商品的3/4时，不仅收回了购买这批商品所付的款项，而且还获得利润90元，这批商品有（）。

A.500件

B.400件

C.300件

D.600件

解法：

设这批商品有x件，卖出了3/4x件。

根据“获得利润90元”，可列方程：

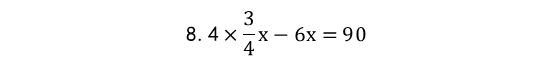
解得x=300。

因此，选择C选项。

例题5

天气预报预测未来2天的天气情况如下，第一天晴天50%、下雨20%、下雪30%；第二天晴天80%、下雨10%、下雪10%，则未来两天天气状况不同的概率为：

A.45%

B.50%

C.55%

D.60%

解法：

根据“第一天晴天50%；第二天晴天80%”，可知：两天每天都是晴天的概率是50%×80%=40%。

根据“第一天下雨20%；第二天下雨10%”，可知：两天每天都是下雨天的概率是20%×10%=2%。

根据“第一天下雪30%；第二天下雪10%”，可知：两天每天都是下雪天的概率是30%×10%=3%。

两天的天气状况相同的概率是40%+2%+3%=45%，则不相同的概率为1-45%=55%。

因此，选择C选项。