例题1

甲车间的生产效率是乙车间的1.5倍，分别生产1200件相同的产品，甲车间所需时间比乙车间少10天，问甲、乙两个车间合作生产3000件相同的产品需要多少天？

A.20

B.25

C.30

D.35

解法：

根据“甲车间的生产效率是乙车间的1.5（3/2）倍”，可设乙车间每天生产的件数为2x，则甲车间每天生产的件数为3x。

根据“生产1200件相同的产品，甲车间所需时间比乙车间少10天”，可列方程：

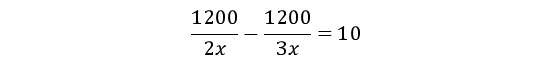
解得x=20。

乙车间的生产效率是2×20=40（件/天），甲车间的生产效率是3×20=60（件/天）。

甲、乙两个车间合作生产3000件相同的产品需要3000÷（40+60）=30（天）。

因此，选择C选项。

知识点：

工作时间=工作总量÷工作效率

例题2

甲、乙、丙、丁四人参加了法律知识竞赛问答活动，四人的平均分为82分，甲、乙、丙三人的平均分为80分，丙、丁二人的平均分为85分，那么丙的得分为：

A.82分

B.85分

C.90分

D.92分

解法：

根据“甲、乙、丙、丁四人的平均分为82分”，可知：甲+乙+丙+丁=82×4=328（分）。

根据“甲、乙、丙三人的平均分为80分”，可知：甲+乙+丙=80×3=240（分）。

丁的得分：（甲+乙+丙+丁）-（甲+乙+丙）=328-240=88（分）。

根据“丙、丁二人的平均分为85分”，可知：丙+丁=85×2=170（分）。

丙的得分：（丙+丁）-丁=170-88=82（分）。

因此，选择A选项。

例题3

某医院内科，今年门诊人数比上一年增加了30%，平均每位患者的门诊花费比上一年下降了20%，若上一年该医院内科门诊收入为3000万元，那么今年的门诊收入大约是多少万元?

A.2600

B.2880

C.3120

D.3640

解法：

根据“今年门诊人数比上一年增加了30%”，可知：今年门诊人数是上一年的130%。

根据“今年平均每位患者的门诊花费比上一年下降了20%”，可知：今年平均每位患者的门诊花费是上一年的80%。

今年门诊收入是上一年的130%×80%=104%。

根据“上一年该医院内科门诊收入为3000万元”，可知：

今年门诊收入是3000×104%＝3120（万元）。

因此，选择C选项。

知识点：

总收入＝人均收入×人数。

例题4

2018年父亲年龄是女儿年龄的6倍，是母亲年龄的1.2倍。已知女儿出生当年（按0岁计算）母亲24岁，则哪一年父母年龄之和是女儿的4倍？

A.2036

B.2039

C.2042

D.2045

解法：

根据“2018年父亲年龄是女儿年龄的6倍，是母亲年龄的1.2倍”，可设女儿年龄为x岁，则父亲年龄为6x岁，母亲年龄为（6x÷1.2）=5x岁。

根据“女儿出生当年（按0岁计算）母亲24岁”，即女儿与母亲年龄差为24岁，可列方程：5x－x＝24，解得x＝6。

故2018年女儿年龄为6岁，父亲年龄为36岁，母亲年龄为30岁。

设t年后父母年龄之和是女儿的四倍。

（36＋t）＋（30＋t）＝4（6＋t），解得t＝21。

故2018＋21＝2039年，父母年龄之和是女儿的4倍。

因此，选择B选项。

例题5

浓度为15%的盐水若干克，加入一些水后浓度变为10%，再加入同样多的水后，浓度为多少？

A.9%

B.7.5%

C.6%

D.4.5%

解法：

根据“加水溶质质量不变”，赋值溶质质量为30克，则浓度为15%的盐水质量为30÷15%=200（克）。

根据“第一次加水之后浓度为10%”，此时盐水质量为30÷10%=300（克）。

故第一次加入的水的质量为300－200＝100（克）。

再加入质量为100克的水，则浓度为30÷（300+100）=7.5%。

因此，选择B选项。

知识点:

溶液质量=溶质质量÷浓度。

浓度=溶质质量÷溶液质量。

溶液质量=溶质质量+溶剂质量。