许多研究人员专注于提高空气静压轴承的刚度和稳定性，但刚度和稳定性之间的矛盾仍然存在。因此，设计了孔板、多孔和多孔限流器，以说明限流器特性对空气静力圆瓦轴承稳定性和刚度的影响。

由于空气静压轴承的刚度和稳定性均由内部压力分布决定，因此采用计算流体动力学（CFD）方法应用完整的纳维-斯托克斯（N-S）方程求解轴承膜中的内部压力分布。仿真结果表明，空气静压圆瓦轴承的刚度和稳定性受几何和材料参数（如膜厚、孔径和粘性阻力系数）的影响显著。

经实验数据验证，孔板限流器的微振动与振幅为0.02 m/s的多个限流器几乎相同，但它比加速度为 0.006 m/s 的多孔限制器强得多，多节流器的最佳刚度提高了46%，而孔板限流器的最佳刚度仅为30.2 N/μm，多孔限流器在小于6 μm的小膜厚中具有明显优势，而最佳刚度提高到38.3 N/μm。数值和实验结果为提高空气静压轴承的刚度和稳定性提供了指导。

空气静压轴承几乎无摩擦，驱动功率低，运动精度高，已广泛应用于超精密机床。关于空气静压轴承的静态和动态特性，刚度和稳定性在实现纳米级运动精度方面起着关键作用。Hoo等人指出，超精密微型铣床需要高刚度的空气静压轴承，以便在存在较大的切削力时保持高精度。

Gao等人指出，高速空气静力主轴的刚度和振动对于超精密微型铣床至关重要。Yuan等人提出，超精密机床的制造精度依赖于空气静压轴承的刚度和稳定性。Wang等人证明了轴承振动对超精密金刚石车削中高精度光学元件的加工精度有重大影响。An等人研究了空气静压轴承主轴的稳定性对用于加工大直径光学元件的超精密飞切机加工精度的影响。

在空气静压轴承中的各种限流器类型中，孔板式限流器因其设计简单、制造成本低而受到广泛关注。Gao等研究了腔室形状对空气静力推力轴承性能特征的影响，发现压力凹陷、气体涡流和湍流强度均随着气膜厚度的减小而减弱。

Li等人描述了带袋孔式限流器的空气静力推力轴承的性能研究，并提出忽略孔长对轴承性能的影响会导致较大的误差。Renn等人重点研究了空气静压轴承中通过孔板式限流器的质量流量特性，并表明通过孔口的质量流量特性与通过喷嘴的质量流量特性不同。

在过去的几年中，已发表的研究主要集中在带孔限制器的空气静压轴承的刚度特性上。Cheng等给出了外压径向轴承设计的选择策略，指出空气静压轴承的刚度随着供应压力的增长而明显增加。Chen等人研究了工况和几何参数对空气静力轴颈轴承刚度的影响，发现含气几何形状对刚度有显著影响。Neves等人对放电系数对空气静力径向轴承刚度性能的影响进行了理论研究。Du等人研究了均压槽对外加压气体径颈轴承负载能力和刚度的影响。

各种结构设计用于增加空气静压轴承的刚度。其中之一包括矩形凹槽，与没有凹槽的设计相比，显著提高了刚度，优于球形凹槽。然而，增加带节流圈的空气静压轴承的刚度也会增加微振动。Bhat等人研究了基于孔板的固有补偿平板空气轴承系统的静态和动态特性，并提出了在高压下容易发生气锤不稳定的情况。

Nishio等人分析了具有小进给孔的空气静力推力轴承的静态和动态特性，并证实具有小进给孔的空气静力推力轴承比带有复合限流器的轴承具有更大的刚度和阻尼系数。Wang等人关注冲击波与边界层的相互作用，这导致了空气静力轴承与孔板限制器的不稳定。Xiong等研究了静水主轴旋转误差运动的机理，发现刚度的增加导致稳定性的降低。

许多研究人员研究了空气静压轴承微振动背后的机制。Chen等人证明微振动与空气静压轴承进气口附近出现的空气涡流密切相关，这些空气涡旋的强度可以通过从涡流边缘到其中心的压降来表示。Mohamed和Yoshimoto指出，在从亚音速到超音速的过渡过程中发生了冲击波，层流和湍流之间的气流过渡导致轴承间隙中的压降和恢复。迄今为止，还没有合适的方法来解决带孔限制器的空气静压轴承刚度和振动之间的矛盾关系。

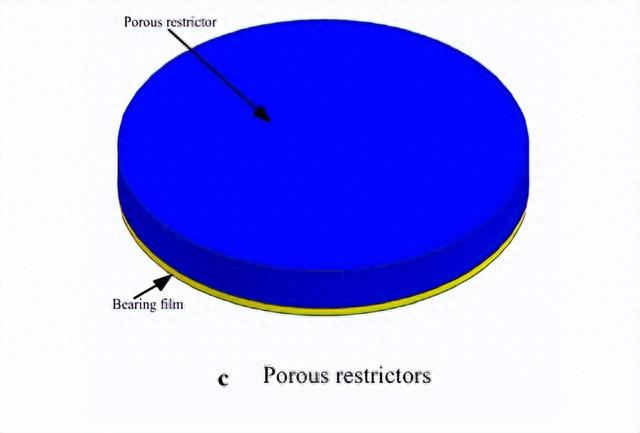
为了克服孔板限流器的缺点，报道了使用多孔限流器和多个限流器的使用。Panzera和Otsu表明，使用多孔材料作为轴承限制器具有在整个轴承表面上更均匀的压力分布的好处，从而产生更高的负载能力，刚度，阻尼和更广泛的稳定性。

Charki等人发现，由于进气口附近的压降较小，因此可以提高具有多个限流器的空气静压轴承的刚度。已发表的文献表明，没有全面的研究考虑不同限流器特性对空气静压轴承刚度和稳定性的影响。与孔板限流器相比，本文设计了多孔限流器和多重限流器，以提高空气静力圆瓦轴承的稳定性和刚度。考虑到空气静压轴承的刚度和稳定性均由内部压力分布特性决定，采用CFD研究了多种不同限流器轴承间隙中的压力分布。

用于计算空气静压轴承流场特性的主要方法包括有限元法（FEM），有限差分法（FDM）和CFD法。雷诺方程可以通过有限元和FDM有效地求解。然而，由于雷诺方程需要大量的假设和简化，即使辅以三区理论，也无法解释气体入口附近的压降和恢复现象。

对于稳态流动和可压缩流体，微观流动特性可以通过完整的3D N-S方程有效捕获。本研究采用基于CFD方法的FLUENT软件求解N-S方程，选取k − ɛ模型计算湍流。RNG模型中包含了涡流对湍流的影响，可以提高入口附近涡流的精度。因此，在 k − ɛ 模型中选择了 RNG 模型，而 C1和 C2分别设置为 1.42 和 1.68。

在以前的许多研究中，空气静力圆瓦轴承的结构被简化为轴对称模型或周期对称模型。图2显示了用于孔板限流器、多节流器和多孔限流器的计算网格和边界条件。本研究采用轴向对称模型分析了带孔板限流器和多孔限流器的空气静压圆瓦轴承的特性，为缩小计算规模，提高计算效率。

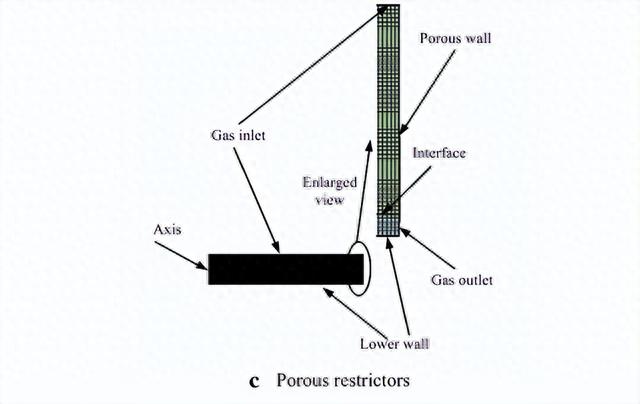
关于多孔限制器，界面被定义为多孔区域和气膜区域之间的链接。为多个限流器选择了周期对称模型，如图2（b）所示，并且只需要三分之一的几何结构即可进行计算。在气膜方向上需要至少四层厚的网格以保证收敛。在计算之前，必须测试网格的独立性，以确保仿真结果的准确性。我们列出了三种不同类型的限流器的计算条件。

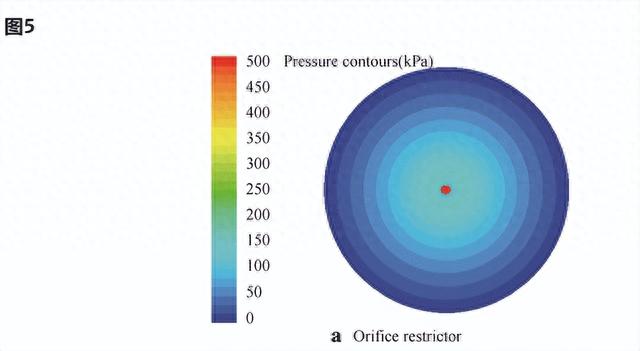
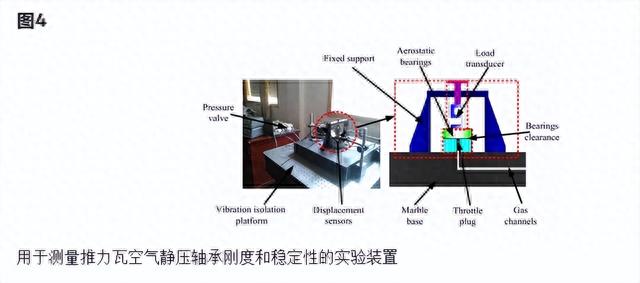
图4显示了测量推力瓦空气静压轴承刚度和稳定性的实验设置。为了尽量减少对环境的干扰，测量设备位于隔振平台上，并在其大理石底座上测试了推力瓦空气静力轴承。固定支架用于保持载荷传感器和空气静压轴承的位置。由阀门调节的加压气体通过大理石底座中的气体通道进入空气静压轴承。节气门塞用于在不同的限流器类型之间切换。施加在空气静力轴承上的力可以通过载荷传感器精确测量。薄膜厚度的变化由位移传感器（TESATRONIC TT80）测量，其数字分辨率为10 nm。位移传感器以相等的间隔安装在空气静压轴承的上边缘。

使用灵敏度为10 mV/g的加速度传感器（AD10T）在相同的三个位置测量每个空气静压轴承的稳定性。加速度值反映了空气静压轴承的稳定性。在稳定性测试期间，空气静压轴承的轴保持静止。

本文在FLUENT软件中选取了SIMPLE算法、理想气体模型和双精度压力求解器。基于薄膜厚度h = 6 μm、孔板限制器直径d = 0.1 mm、工作压力100 kPa、入口气体压力500 kPa和出口气体压力0 kPa，使用后处理功能获得了流体域压力分布的3D视图，如图5所示。

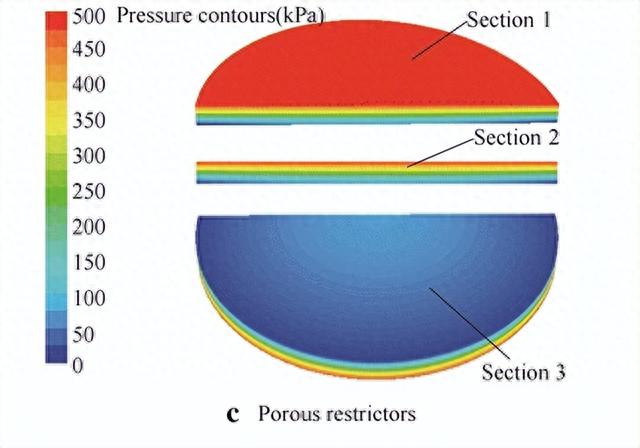
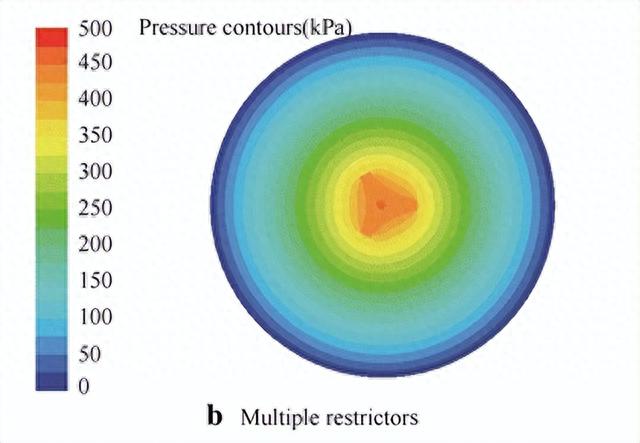
根据计算出的节流阀压力分布，限流器入口处的压力急剧下降，然后从入口到出口平稳下降。多个限流器的压力分布表明，多个腔室的存在对保持高压的能力有显著影响。高压下气膜表面面积明显增大。图5（c）显示了多孔限流器的压力轮廓。在此图中，第 1 节显示了多孔材料上表面的压力，第 2 节表示沿中心的二维 （2D） 压力分布，第 3 节显示了轴承游隙中的压力分布。根据多孔限流器的压力分布，很明显，轴承间隙中的压力分布比孔板中的压力分布更均匀，因为多孔材料的表面包含无数的小孔。

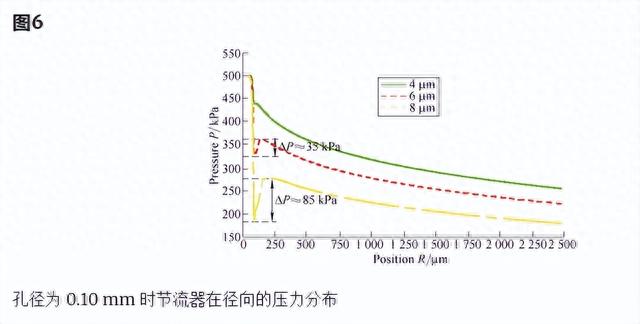
孔径为0.10 mm的孔板限制器径向的压力分布特性如图6所示。准确捕捉了进气口附近的压降和恢复现象。在本文中，∆P定义为压降和恢复现象的强度。很明显，∆P从0增加到近85 kPa，这意味着空气静压轴承随着油膜厚度的增加而变得不稳定。

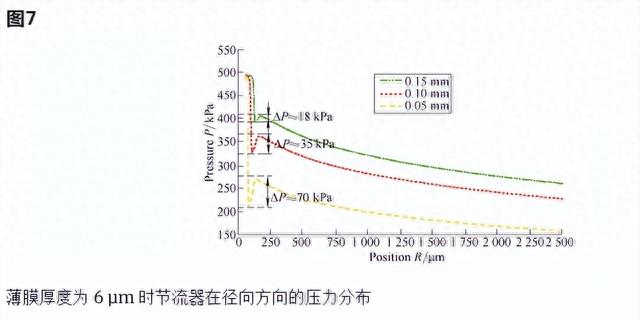
在相同条件下（薄膜厚度h = 6 μm），限流器直径（0.05 mm、0.10 mm、0.15 mm）对压力分布特性的影响如图7所示。随着孔板限流器直径的减小，∆P 从 0.18 增加到 70 kPa，导致空气静压轴承不稳定。许多研究人员已经证明，空气静压轴承的不稳定性与轴承入口附近出现的空气涡流密切相关，空气涡旋的强度可以通过涡流边缘与其中心之间的压降来表示。空气涡流的强度随着供应压力的增加而增加。空气静压轴承的稳定性问题不能通过改变孔板限制器的直径、长度或凹槽形状来有效解决。

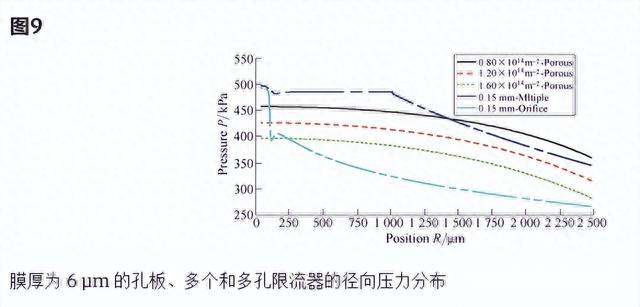
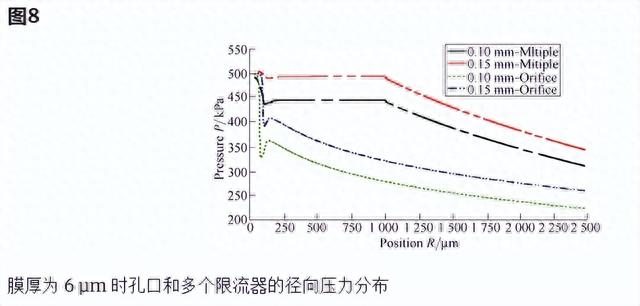
然而，与孔板限制器相比，多个限制器明显显示出更低的压降，如图8所示。因此，理论上可以有效提高具有多个限流器的空气静压轴承的负载能力和稳定性。对于多孔限流器，径向的压力分布特性如图9所示。在进气口附近没有发生压降和恢复现象。

由于多孔材料表面普遍存在小孔，轴承间隙中的压力分布比孔板限流器和多个限流器更均匀。因此，多孔空气静压轴承表现出更好的稳定性。在亚音速流动条件下，粘性阻力系数的影响远大于惯性阻力系数的影响。在膜厚h=6μm和供气压力为500kPa的条件下，粘性电阻系数（0.8×1014m−2， 1.2 × 1014m−2， 1.6 × 1014m−2）上的压力分布特性也示于图9。随着粘性阻力系数的减小，轴承游隙内的压力分布显著改善。

当薄膜厚度小于6 μm时，多孔限制器显然更具优势。相对于孔板限流器的最佳刚度为15.71 N/μm，多孔限流器的最佳刚度显著提高，为40.46 N/μm。图显示了具有不同类型限流器的推力瓦空气静压轴承的实验加速度。多个限流器的微振动，加速度为 0.015 m/s2，弱于节流板，其加速度为0.02 m/s2，但比多孔限流器强得多，多孔限流器的加速度为0.006 m/s2.

推力瓦空气静压轴承的刚度和稳定性受几何和材料参数的显著影响。对于孔限流器和多节流器，刚度逐渐增加到最大值，然后随着膜厚的增加而降低。然而，对于多孔限制器，它持续降低。

多节流器的最佳刚度明显优于孔板限流器30.34 N/μm。多孔限制器在薄膜厚度小于6μm时具有明显的优势。与孔板限流器相比，多孔限流器的最佳刚度可以从15.71 N/μm提高到40.46 N/μm。多个限流器的加速度，0.015 m/s2，弱于孔板限制器，0.020 m/s2，但比多孔限制器强得多，其值为 0.006 m/s2.结果表明，多孔限流器比多限流器和孔板限流器具有更好的稳定性。