文｜凝妈悟语

在过去的考试中，孩子在做按顺序填数字时，遇到过两次没有思路的情况。

第一次：31，34，37，（），（）。

一眼看不出规律，数字不连续，也不像紧随其后的题目，都是整数，早在幼儿园时期就非常熟悉，因为看数字积木看的多，自然就记住了。

第二次：78□70□□

两个数字不相邻，无法套用以前计算两个数差值的方法，又该怎么找规律呢？不知从何入手！同样的，前面的都是差5，也是幼儿期天天念叨的规律。

畏难情绪严重！

每次看到新题目，就感到害怕，认为自己不会做，没有动力用已有的知识思考解决，直接撂挑子。

规律识别困难！

不知道这些题目其实是考查连续加减，不会进行知识转化，不懂如何灵活运用。

观察和归纳能力不足！

没有养成逐项对比、标记变化的习惯，导致难以发现规律。

总之就是学习动力不足、解决问题能力欠缺、基础不扎实，缺练。

目前来说，这类题目还停留在“规律连续且一致”的层面，还没有出现交替变化，学起来并不难。

首先，提升解题自信。

要让孩子知道，学校里考到的题目不会超纲，不过也不会和课本上的题目一模一样，会有很多变化，但都可以用已有知识去解决，让孩子充满信心挑战看起来有些难的题目。

像这类题目，其实就是课本51页的“连续减一个数写出差值”，在考试中会改变被减数和减数出现同类题，也会换个形式摇身一变成“按顺序填数字”，算法都是一样的。

帮孩子建立知识点的链接，就从很大程度上消除畏难情绪。

其次，分步引导。

问孩子：谁比谁大几？根据具体题目调整问法，帮助孩子发现固定差值。

比如，

问：34比31大几？37比34大几？有什么共同之处？

孩子能算出差值都是3，从而知道后面的空格内是相邻数字+3。

问：78比70大几？中间可以填哪些数？哪个数可以保证增加的是同一个数？

孩子能算出差值是8，枚举出77、76、75、74、73、72、71。计算发现74合适，78-74=4，74-70=4。

进一步引导，4是不是正好是8的一半，为后面的归纳总结打基础。

在纸上画出相邻数的增减，标记变化，观察连续加减一个数的规律。

还可以用数棒或积木块具象展示，让孩子看到数字的直观变化。

依次摆出增加的数量，或者依次拿走减少的数量，感受数字的增加和减少。

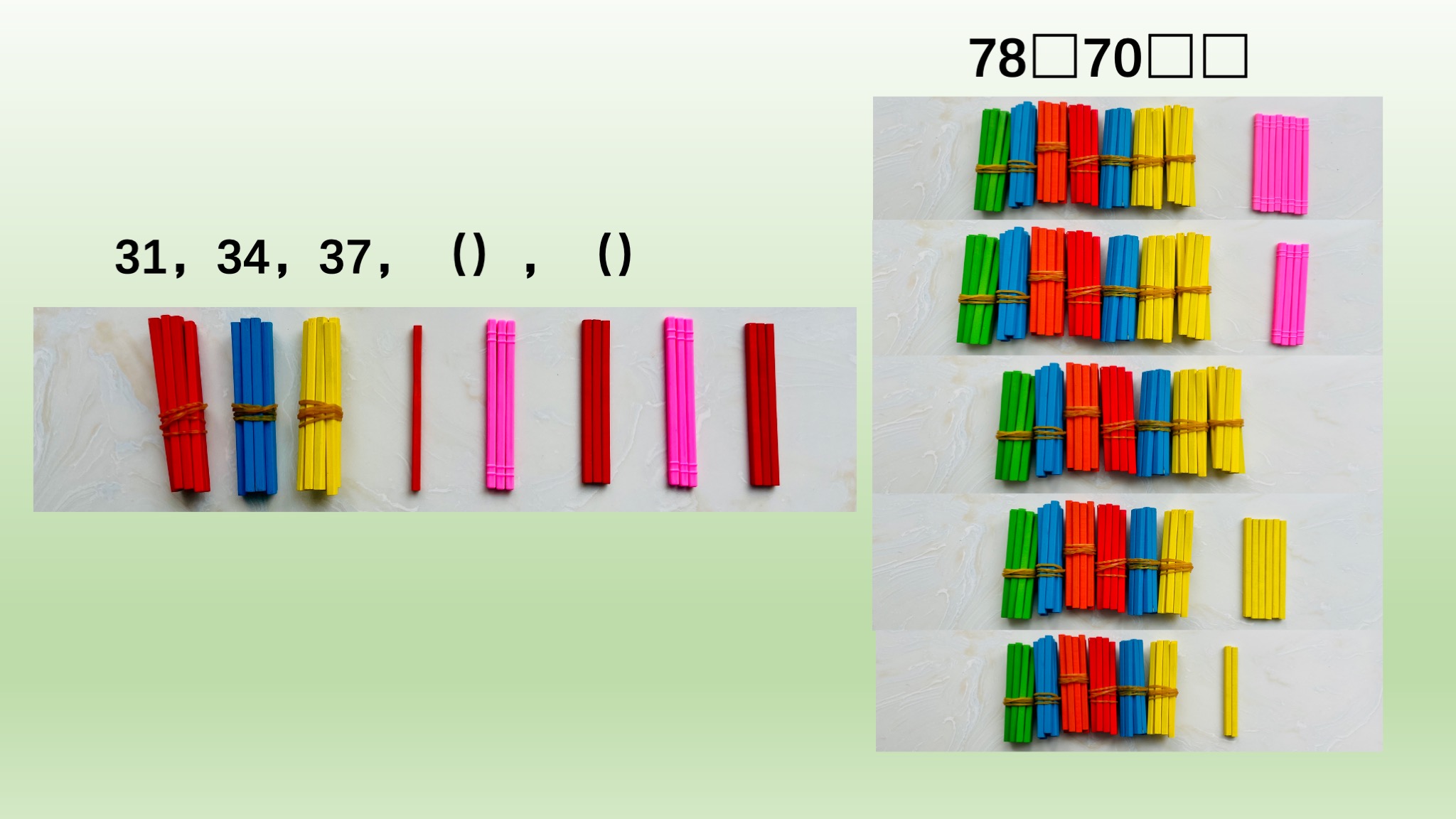
最后，规律归纳训练。

归纳做题步骤，有条理地解决问题。

第一步，观察数字是递增还是递减。递增是加同一个数，递减是减同一个数。

第二步，计算相邻两个数之差，找到每次增加或减少的数字。

若两数连续，计算一次即可。

若两个数中间有一个空格，需计算两次。两数相减后，再想差值的一半是多少。（上学期已经学过一半的概念，孩子也能理解）。

第三步，按照增减规律，加减第二步计算出的差值，填入空格内。

第四步，验算差值。计算每两个相邻数的差值，看是否是同一个数。

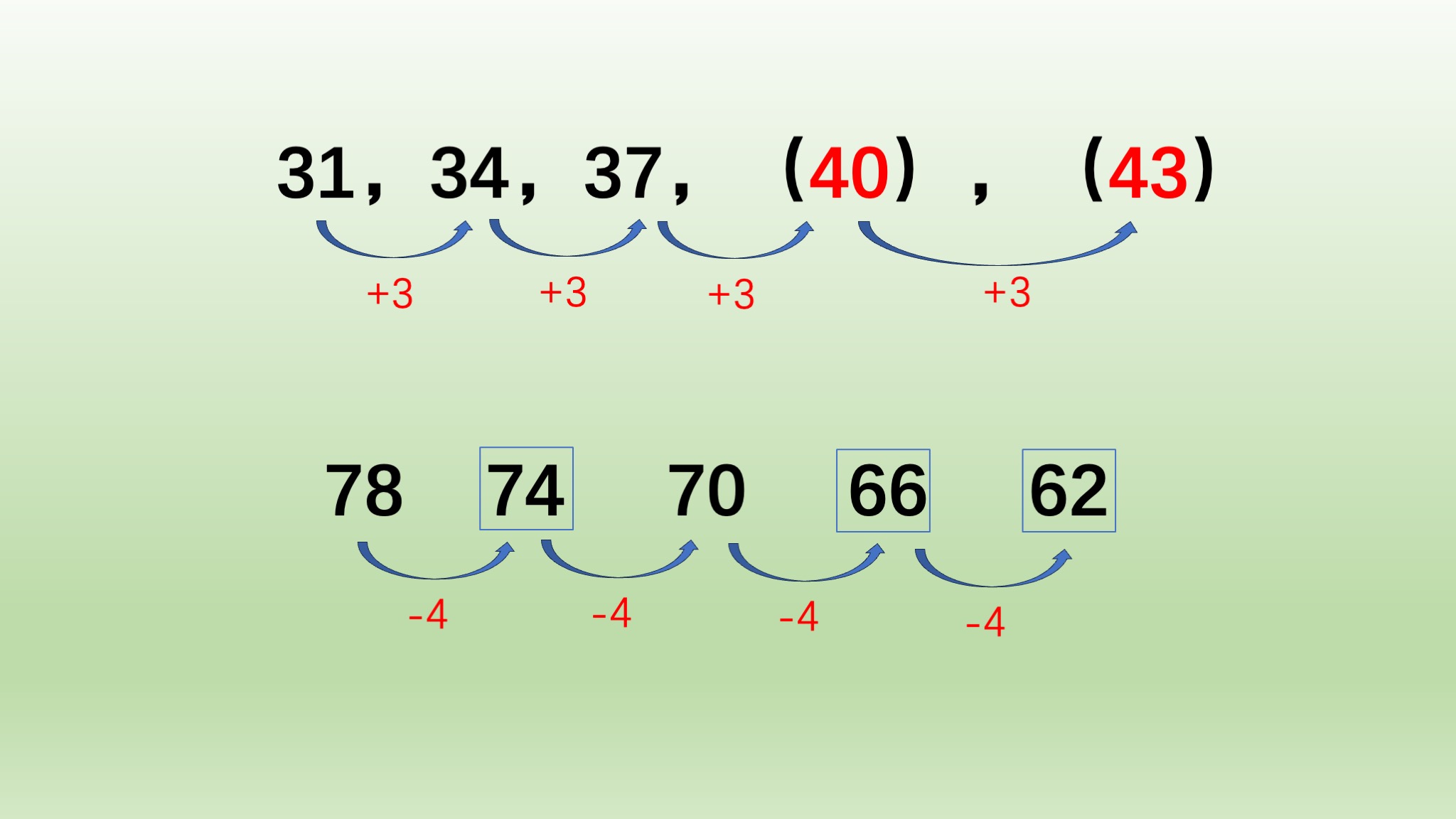
按以上步骤解答“31，34，37，（），（）”。

数字越来越大，是每个数增加一个数。

34-31=3，37-34=3。

那么37后面是37+3=40，40后面是40+3=43。

43-40=3，40-37=3，差值一致，正确。

按以上步骤解答“78□70□□”。

数字越来越小，是每个数减少一个数。

78-70=8，8的一半是4。

那么78后面是78-4=74，70后面是70-4=66，66后面是66-4=62。

78-74=4，74-70=4，70-66=4，66-62=4，差值一致，正确。

孩子理解了这类题目的做法，明确了做题步骤，但是不经过重复训练，也只是浅尝辄止。随着时间的推移，孩子的理解记忆也会变得模糊，所以还要找同类题目进行练习，培养观察和思考习惯，提升能力。

为孩子找了部分练习题，可以练习巩固。

写在最后：

一年级数学，按顺序填数字，并不是很复杂的问题，但是因为孩子见得少，容易卡壳，要帮助孩子克服畏难情绪并打开思路。

根据孩子的认知特点，通过和联系课本知识、提问引导、直观演示、针对性练习，能让孩子逐步掌握规律分析，提升解题信心，提高做题准确率。