例题1

从一个装有水的水池中向外排水，规定每周二、四、六每天排出剩余水量的1/3，其余日期每天排出剩余水量的1/2。如此连续操作6天后，水池中剩余相当于总容量1/72的水。问最开始时水池中的水量最多相当于总容量的：

A.1/2

B.5/8

C.1/4

D.3/8

解法：

设最开始时水池中的水量最多相当于总容量的y。

排出剩余的水量的1/3，可知：剩余水量占1-1/3=2/3。

排出剩余的水量的1/2，可知：剩余水量占1-1/2=1/2。

根据“连续操作6天后”，可知：这连续六天分为两类情况。

情况一：3天排出剩余的水量的1/3和3天排出剩余的水量的1/2。

例如：周二、周三、周四、周五、周六、周日。

解得y=3/8。

情况二：2天排出剩余的水量的1/3和4天排出剩余的水量的1/2。

例如：周日、周一、周二、周三、周四、周五。

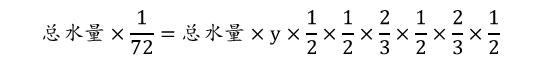
解得y=1/2。

3/8<1/2。

因此，选择A选项。

例题2

“数艺杯”绘画比赛的决赛规则如下：由3位评委对11件作品进行投票，每位评委对每件作品可以投一票或者不投票；得3票的作品为一等奖，得2票的作品为二等奖，得1票的作品为三等奖，不得票的作品为鼓励奖。已知三位评委分别投出了6票、7票、8票，且有3件作品为鼓励奖，那么（）。

A.一等奖作品比三等奖作品多5件

B.一等奖作品比二等奖作品多2件

C.二等奖作品比一等奖作品多5件

D.二等奖作品比三等奖作品多3件

解法：

设一等奖作品有x件，二等奖作品有y件，三等奖作品有z件。

根据“三位评委分别投出了6票、7票、8票”，可知：三位评委投票共计6+7+8=21（票）。

根据“有3件作品为鼓励奖”，可列方程：x+y+z=11-3①。

根据“得3票的作品为一等奖，得2票的作品为二等奖，得1票的作品为三等奖”，可列方程：3x+2y+z=21②。

②-①×2，得x-z=5。

即一等奖的作品比三等奖的作品多5件。

因此，选择A选项。

例题3

甲、乙两个学校的在校生人数之比为5:3，甲学校如果转入30名学生，再将85名学生转到乙学校，则两个学校在校生人数相同。则此时乙学校学生人数在以下哪个范围内?

A.不到200人

B.在200—240人之间

C.在241—280人之间

D.超过280人

解法：

根据“甲、乙两个学校的在校生人数之比为5:3”，可设甲学校的在校生人数为5x人，乙学校的在校生人数为3x人。

很久题意可列方程：5x+30-85=3x+85。

解得x=70。

则此时乙学校学生为3x+85=210+85=295（人）。

因此，选择D选项。

例题4

某单位后勤部门采购了一批大米，并将其平均分给了甲、乙两个饭堂。5周后，甲饭堂只剩余大米7千克；又过了1周，乙饭堂也只剩余大米6千克，已知甲乙饭堂的就餐人数固定，前往甲饭堂就餐的人数比乙饭堂多1人。如果每人每周消耗大米1千克，则这批大米共有（）千克。

A.72

B.84

C.96

D.108

解法：

设乙饭堂的就餐人数为x人，则甲饭堂的就餐人数为（x+1）人。

根据“5周后，甲饭堂剩余大米7千克”，可知甲饭堂原有大米[5（x+1）+7]千克。

根据“6周后，乙饭堂剩余大米6千克”，可知乙饭堂原有大米（6x+6）千克。

根据“一批大米平均分给了甲、乙两个饭堂”，可列方程：5（x+1）+7=6x+6。

解得x=6。

因此这批大米共有2（6x+6）=2×（6×6+6）=84（千克）。

因此，选择B选项。

例题5

某食品厂速冻饺子的包装有大盒和小盒两种规格，现生产了11000只饺子，恰好装满100个大盒和200个小盒。若3个大盒与5个小盒装的饺子数量相等，则每个小盒与每个大盒装入的饺子数量分别是：

A.24只、40只

B.30只、50只

C.36只、60只

D.27只、45只

解法：

设每个大盒装入的饺子数量为x个，每个小盒装入的饺子数量为y个。

根据“11000只饺子，恰好装满100个大盒和200个小盒”，可列方程：100x+200y=11000①。

根据“3个大盒与5个小盒装的饺子数量相等”，可列方程:3x=5y②。

联立①②，解得x=50，y=30。

因此，选择B选项。