例题1

汪先生乘飞机需托运69千克行李，应付行李超重费735元，后在候机室内巧遇2位没有托运行李的好友，他们也乘同一个航班，于是汪先生就将行李作为三人共有，因而只需付135元行李超重费，那么每位乘客可免费托运行李（）千克。

A.20

B.18

C.16

D.15

解法：

根据“行李超重费735元”，“将行李作为三人共有，需付135元行李超重费”，可知：托运费用减少了735-135=600（元）。

那么每位乘客可免费托运行李的费用为600÷2=300（元）。

托运行李的单价为（735+300）÷69=15（元/千克）。

故每人可免费托运的行李重量为300÷15=20（千克）。

因此，选择A选项。

例题2

甲、乙两个单位人数相同，甲单位的党员占总人数的20%，乙单位的党员占总人数的25%。如果乙单位20名党员与甲单位20名群众互换单位，则两个单位党员占比相同。问两个单位共有党员多少人？

A.256

B.288

C.324

D.360

解法：

设甲、乙两个单位的总人数均为20x人。

根据“甲单位的党员占总人数的20%”，可知：甲单位的党员人数为20%×20x，化简得4x人。

根据“乙单位的党员占总人数的25%”，可知：乙单位的党员人数为25%×20x，化简得5x人。

根据“乙单位20名党员与甲单位20名群众互换单位”，可知：

甲单位党员人数为（4x+20）人。

乙单位党员人数为（5x-20）人。

根据“甲、乙两个单位人数相同”，“交换后两个单位党员占比相同”，可知：两个单位的党员人数相同。

可列方程：4x+20=5x-20。

解得x=40。

那么两个单位共有党员4x+5x=9x=9×40=360（名）。

因此，选择D选项。

例题3

某工厂有甲、乙、丙3条生产线，每小时均生产整数件产品。其中甲生产线的效率是乙生产线的3倍，且每小时比丙生产线多生产9件产品。已知3条生产线每小时生产的产品之和不到100件且为质数，则乙生产线每小时最多可能生产多少件产品？

A.14

B.12

C.11

D.8

解法：

设乙生产线每小时生产产品x件，则甲生产线每小时生产产品3x件，丙生产线每小时生产产品（3x-9）件。

3条生产线每小时生产的产品之和为x+3x+（3x-9），化简得（7x-9）件。

根据“3条生产线每小时生产的产品之和不到100件且为质数”，可知：

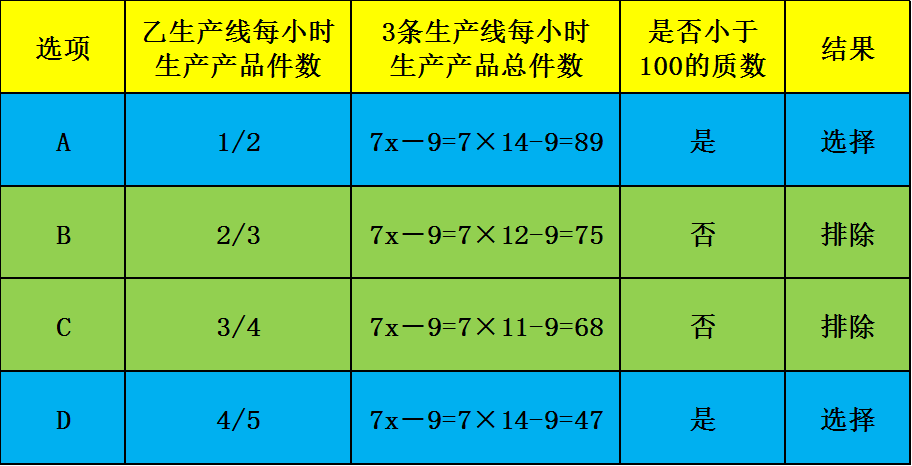
根据“乙生产线每小时最多生产多少件产品”，可知：要求最多，因此乙生产线每小时最多生产14件产品。

因此，选择A选项。

例题4

有A、B两个水壶，分别装有a、b升水。现将B壶中的一半水倒入A壶中，再将A壶中的一半水倒回B壶中。将上述过程记为一次操作，那么两次操作后A、B两壶中的水又回到初始状态，那么a/b=？

A.1/2

B.2/3

C.3/4

D.4/5

解法：

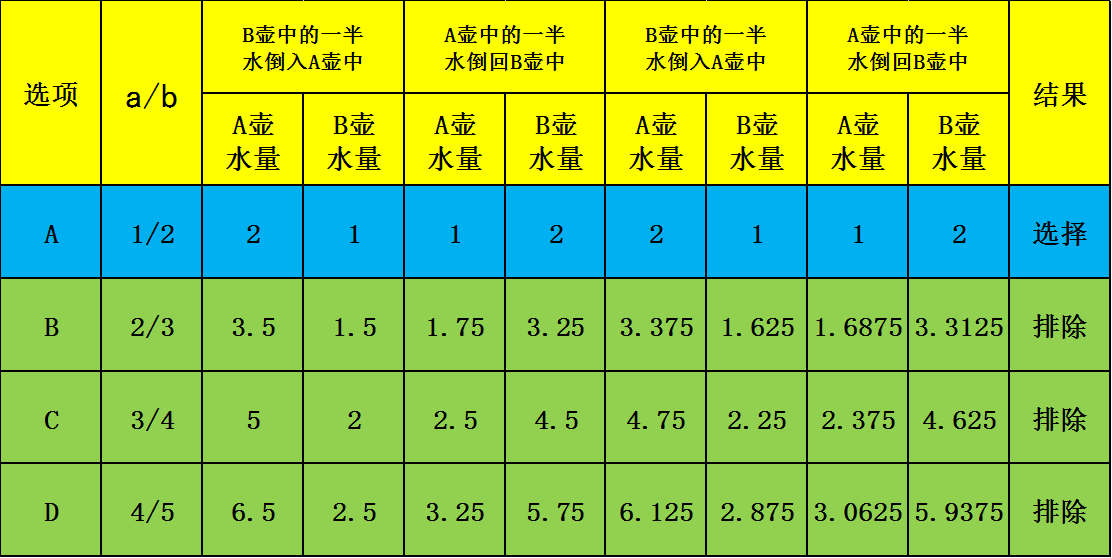
因此，选择A选项。

例题5

某点心铺的糕点按每斤24元销售，周六店庆时按每斤20元销售。如果某单位为举办茶话会在周五、周六共买了33斤的糕点，且两次花的钱相等，那么该单位周五买了多少斤糕点？

A.15

B.17

C.19

D.21

解法：

设该单位周五买了x斤糕点，则周六买了（33-x）斤糕点。

根据题意可列方程：24x=20（33-x）。

解得x=15。

因此，选择A选项。