例题1

甲工程队与乙工程队的效率之比为4:5，一项工程由甲工程队单独做6天，再由乙工程队单独做8天，最后由甲、乙两个工程队合作4天刚好完成，如果这项工程由甲工程队或乙工程队单独完成，则甲工程队所需天数比乙工程队所需天数多多少天？

A.3

B.4

C.5

D.6

解法：

根据“甲工程队与乙工程队的效率之比为4:5”，赋值甲工程队的效率为4，乙工程队的效率为5。

根据“甲单独做6天，乙单独做8天，甲乙合作4天刚好完成”，可知：工作总量为4×6+8×5+（4+5）×4=100。

甲工程队所需天数比乙工程队所需天数多100÷4+100÷5=5（天）。

因此，选择C选项。

例题2

甲去北京出差，去时坐飞机，返回时坐高铁，若飞机的速度比高铁快3倍，且往返平均速度为480千米/小时，问甲乘坐的飞机速度为多少千米/小时？

A.720

B.768

C.960

D.1200

解法：

根据“飞机的速度比高铁快3倍”，可设高铁速度为x千米/小时，则飞机速度为4x千米/小时。

根据“往返平均速度为480千米/小时”，等距离平均公式，可列方程：

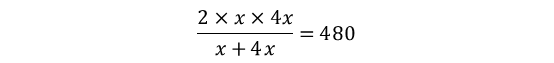
解得x=300，则飞机速度为4x=4×300=1200（千米/小时）。

因此，选择D选项。

知识点：

等距离平均公式：设等距离的长度为单位“1”，第一段距离的速度为v1,第二段速度为v2。则第1段距离用时为1/v1，第二段距离用时为1/v2。平均速度为：

例题3

某股民以每股25元的价格买了一公司的股票2000股，一段时间后，他以每股32元的价格卖掉了70%，剩余的十天后又以每股20元的价格卖出，那么他从这次股票买卖中获得多少元的利润？

A.680

B.4600

C.6800

D.12800

解法：

根据“每股25元的价格买2000股”，“每股32元的价格卖掉了70%”，第一次获得（32-25）×（2000×70%）=9800（元）。

根据“每股20元的价格卖掉了30%”，第二次获得（20-25）×（2000×30%）=-3000（元）。

他从这次股票买卖中获得9800-3000=6800（元）的利润。

因此，选择C选项。

知识点：

利润=售价-成本。

例题4

在统计某高校运动会参赛人数时，第一次汇总的结果是1742人，复核的结果是1796人，检查发现是第一次计算有误，将某学院参赛人数的个位数字与十位数字颠倒了。已知该学院参赛人数的个位数字与十位数字之和是10，则该学院的参赛人数可能是：

A.64人

B.73人

C.82人

D.91人

解法：

根据“第一次汇总的结果是1742人，复核的结果是1796人”，可知：复核结果与第一次结果差值为1796-1742=54。

根据“人数的个位数字与十位数字颠倒了”，可知：

因此，选择C选项。

例题5

某商店出售A商品，若每天卖100件，则每件可获利6元。根据经验，若A商品每件涨1元钱，每天就少卖10件。为使每天获利最大化，A商品应提价：

A.6元

B.4元

C.2元

D.10元

解法：

设A商品涨x元，利润为y元。

根据“每天卖100件，每件可获利6元”，且“每件涨1元钱，每天就少卖10件”，可列方程：y=（6+x）（100-10x），化简得，y=10（6+x）（10-x）。

根据“获利最大化”，可知当6+x=10-x时，y值最大，解得x=2。所以A商品应提价2元。

因此，选择C选项。