例题1

工程师设计某种新能源纯电动汽车，其单位距离理论行驶电耗和车辆自重成正比，车辆搭载的电池组重量和电容量成正比。这种电动汽车除电池组以外的重量为1.5吨，搭载重100公斤的电池组时，满电状态可续航80千米，问这种电动汽车满电状态理论行驶距离要达到500千米的话，全车含电池组的重量在以下哪个范围内？

A.2.3吨以内

B.2.3—2.4吨之间

C.2.4—2.5吨之间

D.2.5吨以上

解法：

赋值单位重量的电耗为1。

1.5吨=1500千克；100公斤=100千克。

根据“搭载重100公斤的电池组”，可知：汽车总重为1500+100=1600（千克）。

根据“电耗和车辆自重成正比”，可知：电耗为1600×1=1600。

故续航80千米的电池容量为1600×80=128000。

根据“电池组重量和电容量成正比”，可知：单位重量电池的容量为128000÷100=1280。

设电池重量为x公斤，则汽车总重为（1500+x）千克，电耗为（1500+x），电容量为1280x。

根据“行驶距离要达到500千米”，可列方程：1280x=500（1500+x）。

解得x≈961.5。

因此汽车总重为1500+961.5=2461.5（千克）=2.4615（吨）。

因此，选择C选项。

知识点：

①1公斤=1千克。

②1吨=1000千克。

③成正比例：两种相关联的量，一种量变化，另一种量也随着变化，如果这两种量相对应的两个数的比值（也就是商）一定，这两种量就叫做成正比例的量，它们的关系叫做成正比例关系。用字母表示：如果用字母x和y表示两种相关联的量，用k表示它们的比值（一定），正比例关系可以用以下关系式表示：k=x/y。

例题2

高中一年级有三个班，一班的学生人数比二班少10%，二班的学生人数比三班多一倍，一班的学生人数比三班多20人，则二班的学生人数为多少人？

A.35

B.45

C.50

D.70

解法：

设二班的人数为x人。

根据“一班的学生人数比二班少10%”，可知：一班的人数为（1-10%）x=0.9x人。

根据“二班的学生人数比三班多一倍”，可知：三班的人数为0.5x人。

根据“一班的学生人数比三班多20人”，可列方程：0.9x-0.5x=20。

解得x=50，即二班的学生人数为50人。

因此，选择C选项。

例题3

村官小刘负责将村委会购买的一批煤分给村中的困难户，如果给每个困难户分300千克煤，则缺500千克；如果给每个困难户分250千克煤，则剩余250千克。为帮助困难户，村委会购买了多少煤？

A.5500千克

B.5000千克

C.4500千克

D.4000千克

解法：

设困难户共有x户。

根据煤总量不变，可列方程300x-500=250x+250。

解得x=15。

故煤的总量为300×15-500=4000（千克）。

因此，选择D选项。

例题4

甲、乙两个仓库共有货物102吨。如果从甲仓库调出3吨到乙仓库，那么甲仓库的货物正好是乙仓库的2倍。则甲仓库原有货物（）吨。

A.31

B.37

C.70

D.71

解法：

设甲仓库原有货物x吨，则乙仓库原有货物（102-x）吨。

根据“甲仓库的货物正好是乙仓库的2倍”，可列方程：x-3=2（102-x+3）。

解得x=71。

因此，选择D选项。

例题5

某地鼓励农户种植果树，规定每个自然年末种植果树面积比年初增加5亩，农民可得到2000元奖金，且超出5亩后每增加1亩可额外获得x元奖金。已知每个自然年种植的果树，从下一自然年起每亩每年可获得y元的果树收入。某农户第一年开始种植果树，当年种植10亩，获奖金3500元；第二年种植面积扩大16亩；第三年种植面积又扩大15亩，年收入比第一年的16倍多1000元。问以下哪个不等式能准确描述x与y的关系？（注：年收入=奖金+果树收入）

A.x＜0.2y

B.0.2y≤x

C.0.5y≤x

D.x≥y

解法：

根据“比年初增加5亩，可得到2000元奖金，超出5亩后每增加1亩可获得x元奖金”，“当年种植10亩，获奖金3500元”，可列方程：2000+（10-5）x=3500。

解得x=300。

根据“第三年种植面积又扩大15亩，年收入比第一年的16倍多1000元”，可列方程：2000+300×（15-5）+（10+16）y=3500×16+1000。

方程解析：

2000表示“比年初增加5亩，农民可得到2000元奖金”。

300×（15-5）表示“超出5亩后每增加1亩可额外获得x元奖金”。

（10+16）y表示“第一年和第二年每亩每年可获得y元的果树收入”。

解得y=2000。

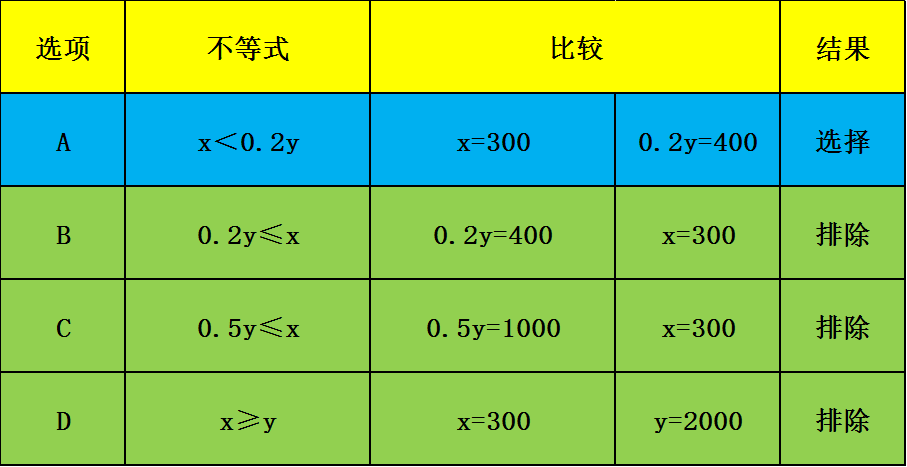
因此，选择A选项。