
例题1

解法:
设乙图书室原有藏书y本,那么甲图书室本数为(y+3x)。
根据“从甲图书室中取出150本书放入乙图书室后,甲图书室的藏书仍比乙图书室多2x本”,可列方程:(y+3x-150)-(y+150)=2x。
解得x=300。
那么甲图书室的藏书比乙图书室多3×300=900(本)。
故甲图书室原有藏书:5000÷2+900÷2=2500+450=2950(本)。
因此,选择C选项。
例题2

解法:
设答对题目数量为x道,答错题目数量为(100-x)道。
根据“小张测试成绩为285分”,可列方程:3x-2(100-x)=285。
解得x=97。
因此,选择D选项。
例题3

解法:
根据“甲和乙两条生产线的效率相同”,可知:甲和乙两条生产线生产件数的差值不变。
根据题意,可列方程组:y-x=x-54①;y-x=1.5x-y②。
解得x=72,y=90。
即9:00~12:00乙一共生产了90件。
那么乙的效率为90÷3=30(时/件),甲的效率与乙的效率相同为30(时/件)。
距离500件还差:500-72-90=338(件)。
需要338÷(30+30)>5.5(小时),即17点30之后。
因此,选择D选项。
知识点:
工作总量=工作效率×工作时间。
工作效率=工作总量÷工作时间。
工作时间=工作总量÷工作效率。
例题4

解法:
根据“第n人(n>1)领取n本,最后一名学生刚巧全部领完,每个学生领到的图书一样多”,代入选项:

因此,选择A选项。
例题5
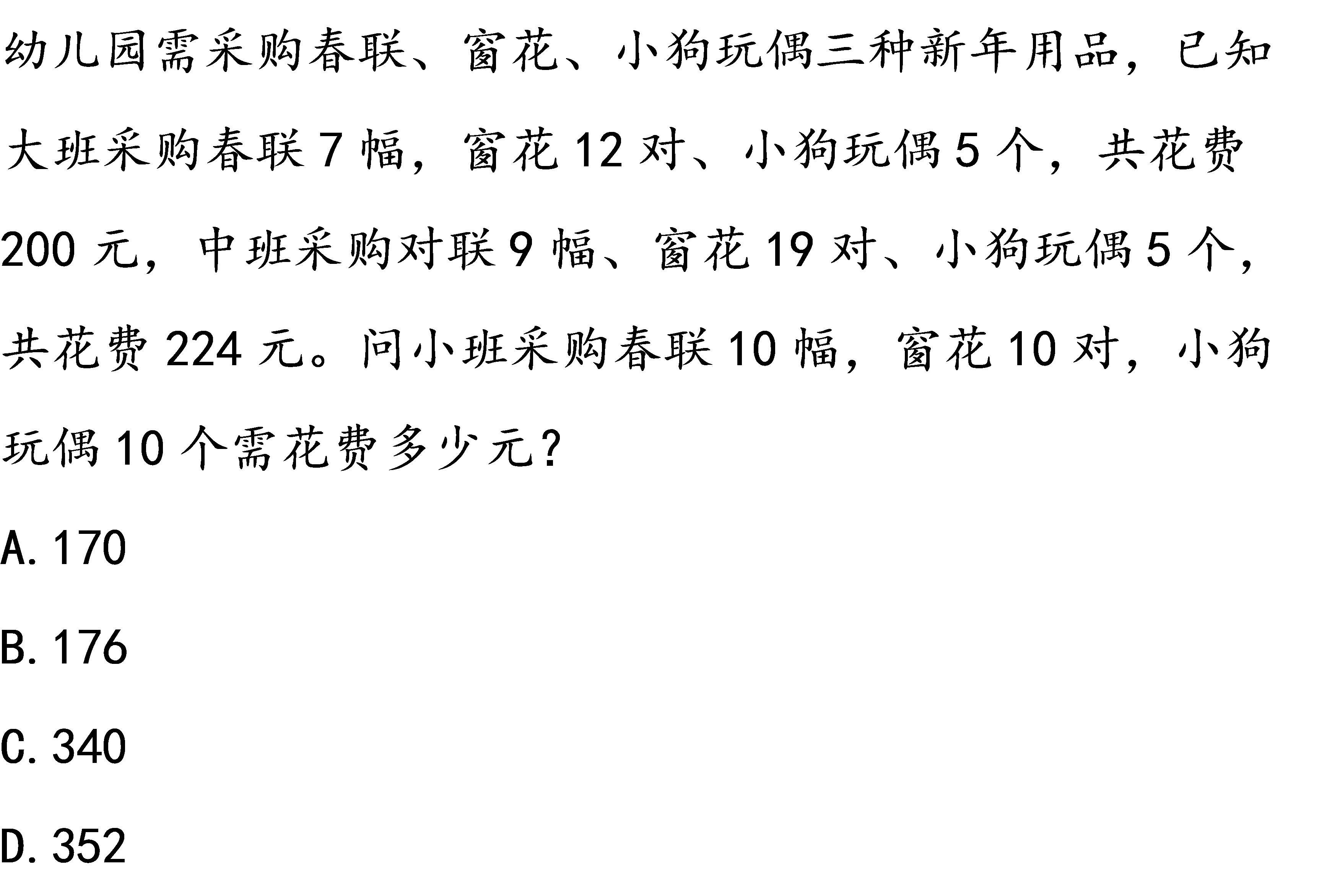
解法:
设一副春联x元,一个窗花y元,一个小狗玩偶z元。
根据题意可列方程组:7x+12y+5z=200①;9x+19y+5z=224②。
假设y=0,解得x=12,5z=116。
则小班需花费:10x+10y+10z=10×12+10×0+116×2=352(元)。
因此,选择D选项。
