例题1

某防疫工作机构有检验人员和其他工作人员共55人，将检验人员平均分成若干个小组开展工作。近期，该机构补充了20位工作人员，其中，检验人员增加了2组，每组人数不变，其他工作人员增加了30%，则该机构原有检验人员共（）组。

A.4

B.5

C.6

D.7

解法：

根据“其他工作人员增加了30%”，可知：其他工作人员补充数=其他工作人员总数×30%=其他工作人员总数×3/10。

则其他工作人员补充数是3的倍数。

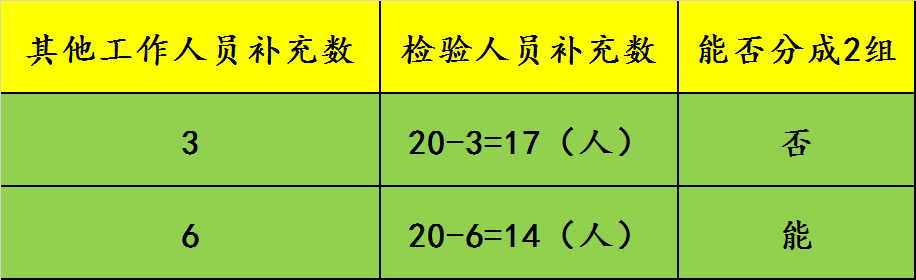
其他工作人员补充数为6人，检验人员为20-6=14（人），每组有14÷2=7（人）。

根据“其他工作人员补充数比其他工作人员数量增加了30%”，可知：原有其他工作人员为6÷30%=20（人）。

那么检验人员为55-20=35（人），可分成35÷7=5（组）。

因此，选择B选项。

例题2

桶中装有一定量的液体，液体体积为桶容量的40%，现向桶中继续加入16升同一液体后，液体体积为原来的1.5倍，则该桶的容量为（）升。

A.20

B.40

C.60

D.80

解法：

设该桶的容量为x升。

根据“液体体积为桶容量的40%”，可知：原来液体的体积为40%x升。

根据“现向桶中继续加入16升同一液体”，可知：现在液体的体积为（40%x+16）升。

根据“液体体积为原来的1.5倍”，可列方程：40%x+16=1.5×40%x。

解得x=80。

因此，选择D选项。

例题3

某餐饮公司甲、乙两种外卖每份的售价分别为30元和50元，若该公司某天售出这两种外卖共500份，销售收入为21400元，则售出的两种外卖数量相差：

A.140份

B.160份

C.180份

D.200份

解法：

设甲售出外卖x份，乙售出外卖y份。

根据“该公司某天售出这两种外卖共500份”，可列方程：x+y=500①。

根据“销售收入为21400元”，可列方程：30x+50y=21400②。

解得x=180，y=320。

售出的两种外卖数量相差320-180=140（份）。

因此，选择A选项。

例题4

现有100升、120升和150升三种容积的油桶共16个，总容积为2030升，其中150升规格的油桶有x个。现将若干个150升规格的油桶换为同样数量的100升油桶，使得100升规格的油桶达到x个，此时所有油桶的容积为1880升，问x的值为多少？

A.2

B.4

C.5

D.9

解法：

设原来100升的油桶有y个，则原来120升的油桶有（16-x-y）个。

根据“现将若干个150升规格的油桶换为同样数量的100升油桶，使得100升规格的油桶达到x个”，可知：150升的油桶换为100升有（x-y）个。

150升的油桶剩余x-（x-y）=y（个）。

根据“总容积为2030升”，可列方程：100y+120（16-x-y）+150x=2030①。

根据“油桶的容积为1880升”，可列方程：100x+120（16-x-y）+150y=1880②。

联立①②，解得x=5，y=2。

因此，选择C选项。

例题5

小王购买某燃油车A，四年行驶6万公里，平均每公里燃油费为0.54元，4年税费和保养费用花费2.3万元，最后以车价的50%卖出。小李以同样的价格购买一款纯电动车B，同样四年行驶6万公里，平均每公里电费为0.14元，4年税费和保养费用花费0.5万元，最后以车价的20%卖出。刚好两人的实际使用费用（实际使用费用=车价+燃油费或电费+税费和保养费-卖出车价）相同。请问小王四年的实际使用费用为多少万元？

A.10.14

B.11

C.12.54

D.14

解法：

设两人购买车的费用均为x万元。

根据“实际使用费用=车价+燃油费或电费+税费和保养费-卖出车价”，可知：

小王的实际使用费用为（x+0.54×6+2.3-50%x）元，化简得（0.5x+5.54）元。

小李的实际使用费用为（x+0.14×6+0.5-20%x）元，化简得

（0.8x+1.34）元。

根据“刚好两人的实际使用费用相同”，可列方程：0.5x+5.54=0.8x+1.34。

解得x=14。

则小王的实际使用费用为0.5x+5.54=0.5×14+5.54=12.54（万元）。

因此，选择C选项。