结合函数的定义域，通过导数知识，解析函数的单调性、凸凹性、奇偶性和极限的性质，进而得到函数的示意图。

对正切函数tanx有，cosx≠0，即：x≠kπ+π/2，则函数的定义域为：{x|x≠kπ+π/2，x∈R，k∈Z}.

∵y=tanx+2x

∴dy/dx=(tanx)＇+2

=sec2x+2>0,即函数y在定义域上为单调增函数。

∵dy/dx=sec2x+2

∴d2y/dx2=2secx*(secxtanx)=2sec2xtanx.

d2y/dx2的符号与tan的符号保持一致。

(1).当tanx>0时，即x∈(kπ,kπ+π/2),

d2y/dx2>0,此时函数为凹函数；

(2).当tanx<0时，即x∈(kπ+π/2,kπ+π),

d2y/dx2<0,此时函数为凸函数。

∵f(x)=tanx+2x

∴f(-x)

=tan(-x)+2(-x)

=-tanx-2x

=-(tanx+2x)

=f(x),即函数为奇函数。

lim(x+→kπ+π/2）tanx+2x=+∞，

lim(x-→kπ+π/2）tanx+2x=-∞。

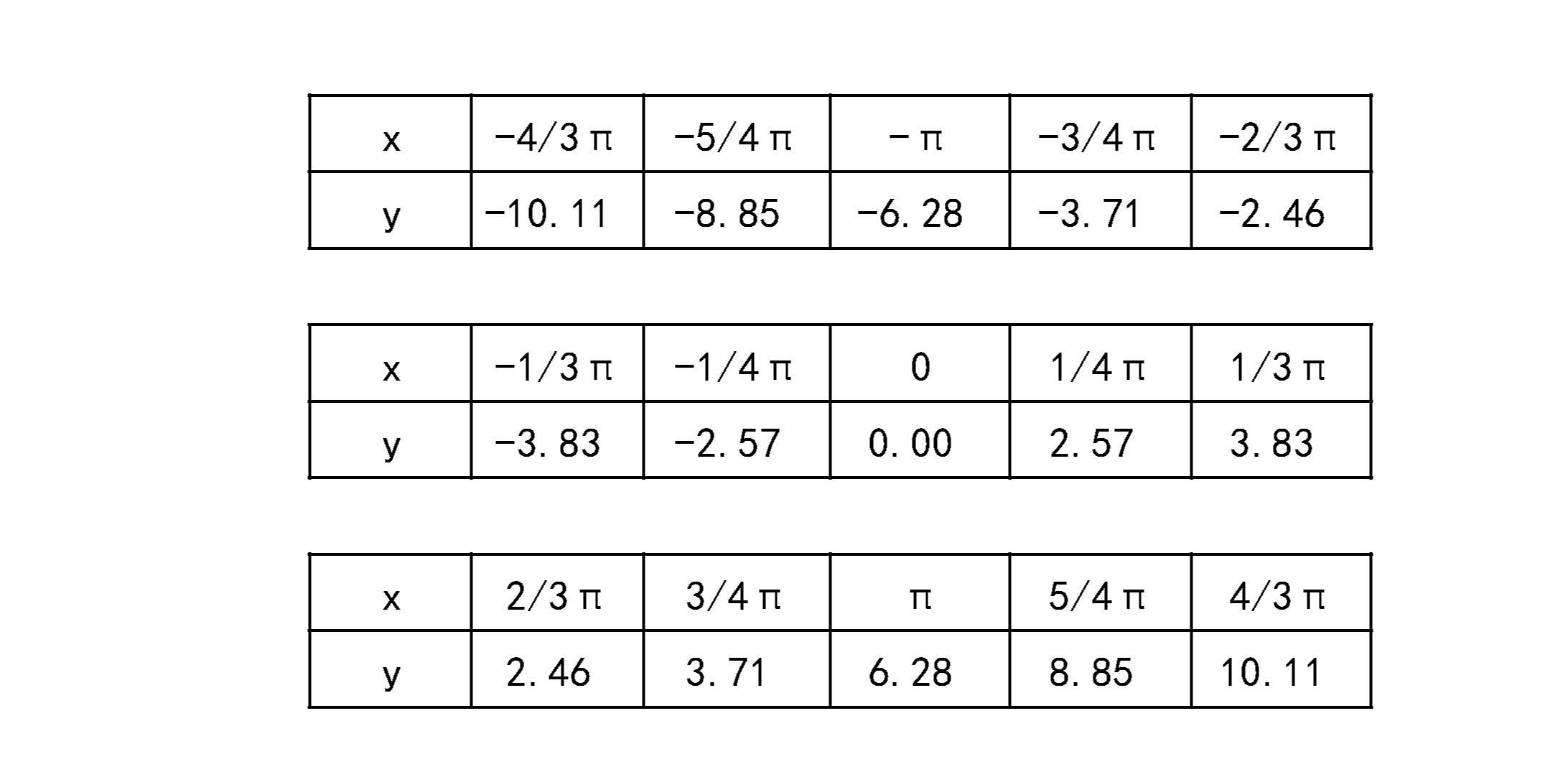
综合上述函数性质，函数的示意图如下所示。