本文主要内容,介绍隐函数y=e^(x+3y)图像示意图的画法和步骤。
※.曲线方程的定义域曲线方程表达式为y=e^(x+3y),即y>0,且lny=x+3y,
则:x=lny-3y.
设x=F(y)=lny-3y,把y看成自变量,求导得:
F'(y)=(1/y)-3=(1-3y)/y.
令F'(y)=0,则y=1/3.
当0<y<1/3时,F'(y)>0;当y>1/3时,F'(y)<0.
所以,当y=1/3时,F(y)有最大值,即:
x=F(y)≤F(y)max=-(1+ln3)
x≤-(1+ln3)/1≈-2.10
即曲线方程的定义域为:(-∞,-2.10]。
※.曲线方程的单调性对方程两边同时对x求导,得:
y=e^(x+3y)
y'=e^(x+3y)(1+3y')
y'=e^(x+3y)/[1-3e^(x+3y)]
即:y'=y/(1-3y).
导数y'的符号与(1-3y)的符号一致。
曲线方程的单调性为:
(1).当y∈(0,1/3]时,y'>0,此时曲线方程y随x的增大而增大;
(2).当y∈(1/3,+∞)时,y'<0,此时曲线方程y随x的增大而减小。
※.曲线方程的凸凹性∵y'=-y/(3y-1),
∴y"=-[y'(3y-1)-3yy']/(3y-1)^2
=-y'/(3y-1)^2
=1^2y/(1-3y)^3
则y"的符号与(1-3y)的符号一致。
曲线方程的凸凹区间为:
(1).当y∈(0,1/3]时,y">0,此时曲线方程为凹曲线;
(2).当y∈(1/3,+∞)时,y"<0,此时曲线方程为凸曲线。
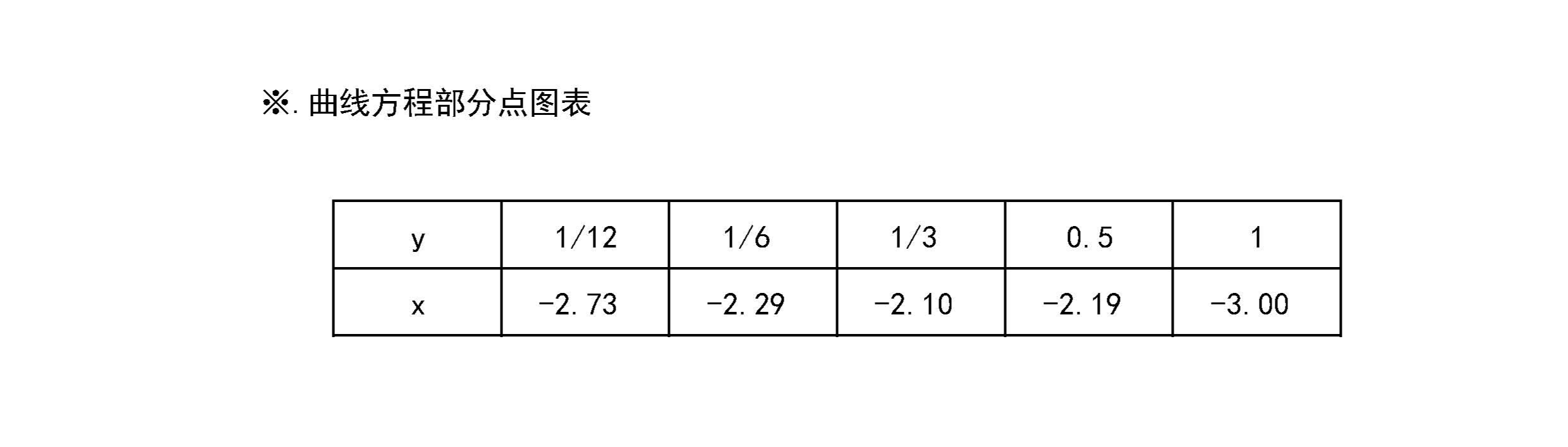
※.曲线方程的五点表