​​

这是一道某地中考模拟测试数学压轴题：正确率不足5%！如图，

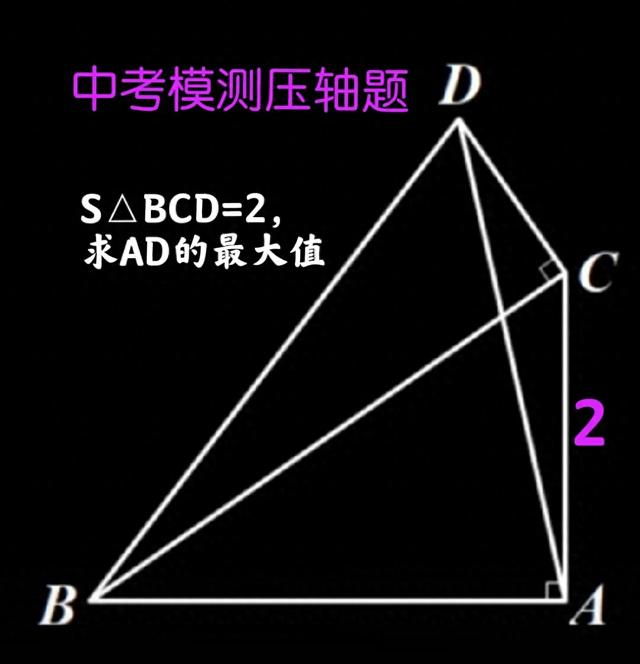
图一

△BAC和△BCD均为直角三角形，AC=2，S△BCD=2，求AD的最大值。

——————————

提示一：射影定理（或三角形相似）+图形旋转（三角形全等）+勾股定理！适合初中生

解题关键：找出暗含条件“CE=CD”，点E为△ABC底边BC上高的垂足。

①过点A作BC垂线AE，由射影定理（或△ACE∽△ABC）可得CE×BC=AC²=4，如图二

图二

②由S△BCD=2可得BC×CD=4=CE×BC，故CD=CE。

③将直角△ACE绕点C顺时针旋转90°后可得直角△CDF，CF=AC=2，即点D轨迹为以CF为直径的圆周。

④当AD经过圆心O时取到最大值，此时AD=OD+OA=1+√5。

或

④'记CF中点为O，由三角形两边之和大于第三边可得AD≤AO+OD（等号当且仅当O、A、D共线时成立）。

提示二：补齐长方形+等积代换+勾股定理！或可适合小学生

①以CD和BC为边作长方形BCDE，如图三

图三

②过点C作AB的平行线与DE相交于点F，则S△ACF=S△BCF=1/2S长方形BCDE=S△BCD=2，从而CF=2。余下步骤同于提示一。

———————————

友友们，怎么看？欢迎留言分享！