为什么蚊子能跟得上速度飞快的高铁?这个问题看起来很简单,实际非常复杂。请允许我慢慢道来,在解构这个谜题的过程中,你也许会惊叹于其中涉及的广泛科学原理。

我们先来探讨一个相对容易理解的场景:当火车保持恒定的速度行驶时,蚊子为何能轻松地飞翔并紧跟高铁的速度?
想象一下,如果蚊子一直停留在火车上,等到火车速度稳定后再起飞,这时,作用在蚊子身上的力与它在地面上的情况并无二致。因为此时,火车与空气已经形成了一个统一体,与蚊子发生互动的只有火车周围的空气,它们都处于相同的惯性参考系中。
牛顿的第一运动定律,在初中物理课本中就有涉及,它指出所有物体都有保持原有运动状态的性质,即惯性。当物体不受外力作用时,它会保持静止或匀速直线运动。

你在这种情况下跳跃,每次落下的位置都是固定的,无论在空中停留多久,蚊子同样如此。
若此时高铁突然开始加速,停在空中的蚊子会被推向车尾吗?答案是:不会。
那么,此时蚊子处于何种状态呢?答案是:蚊子会稍微倾斜,保持悬停状态。
接下来,让我来详细解释这个现象——
在此之前,我们需要介绍一个在初高中未曾提及的概念——惯性力。

前面提到,惯性是物体保持静止或匀速直线运动状态的属性,它并非力,而是每个物体所固有的性质。当物体进行变速运动时,为了方便计算,我们虚构出一个力,称为惯性力,这个力没有施力物体,方向与加速度相反。变速运动所处的参考系称为非惯性参考系。
惯性力的计算公式与重力公式G=mg相同,只需用加速度替换重力加速度g,从而计算出物体在加速度作用下的惯性力。以高铁为例,其加速度通常在0.2m/s²左右,蚊子的质量约为2毫克,因此其惯性力约为4*10的负七次方N。

在非惯性参考系中,以高铁车厢为参照物,由于高铁的加速度,蚊子会产生一个与高铁运动方向相反的惯性力。这个力与重力垂直,它们合成的合力位于这两个力夹角之间,力越大,合力越偏向该力。
力的大小是通过勾股定理,即初中数学中的重力平方加上惯性力的平方再开方得到。

对于蚊子来说,这一过程相当于重力出现了轻微的偏移,大小也略有增加。蚊子会觉得自己正在垂直向下扇动翅膀,但实际上已经偏向下方。蚊子的上升力则朝向高铁车头的斜上方,与合力方向相反。

这里有一个思考题,请你们尝试回答:如果你站在公交车上,公交车突然加速,在你没有失去平衡的情况下,身体会倾向于哪个方向倾斜?
答案是:车头。因为如果你没有失去平衡,你肯定会身体前倾以平衡重力和你自身的惯性力。这个合力向下并且偏向车尾。
下次有机会,你可以亲自观察一下这个现象。
到此,我们解答了简单的问题,接下来的内容可能会变得更加复杂,希望你们能跟上。
如果蚊子在飞行过程中随时都能与高铁保持同步,那么,如果我们试图消灭它呢?如果它只是悬浮在空中,并不煽动翅膀呢?
此时,如果高铁正处于加速阶段,你可以想象高铁车头抬起,车厢倾斜。高铁加速度越大,与地面的夹角也越大,而向下的力,相对于重力也会相应变大。此时车厢内物体的运动方向仅与密度有关,密度大于空气的会下降,密度小于空气的则会上升。
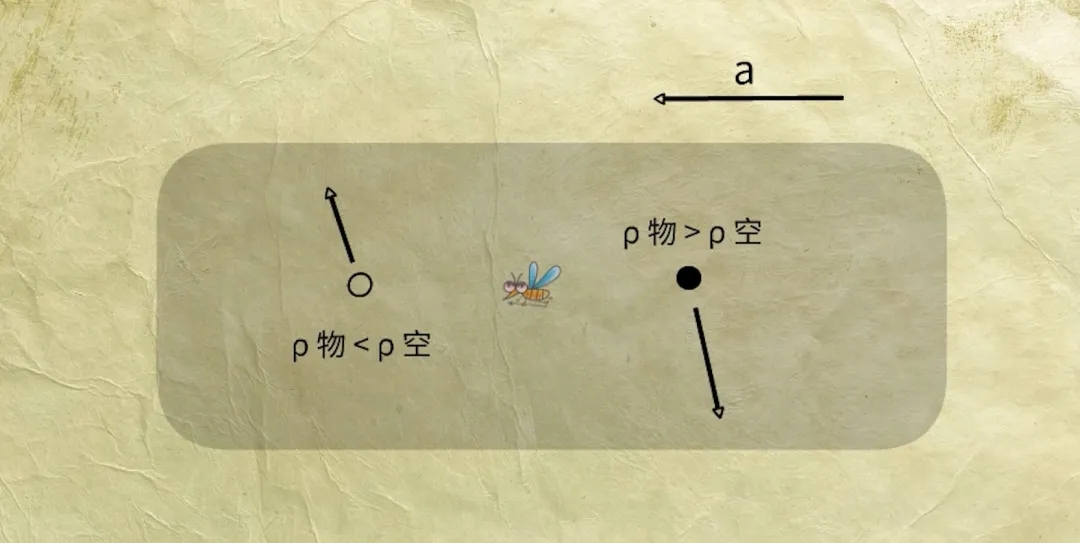
如果我们将高铁放平,密度大于空气的物体会向车尾斜下落,密度小于空气的则向车头斜上上升。
当高铁加速时,如果车厢里有一个玻璃球和一个氢气球,玻璃球会向车尾滚去,而氢气球会在车厢顶部向车头方向蹭去。
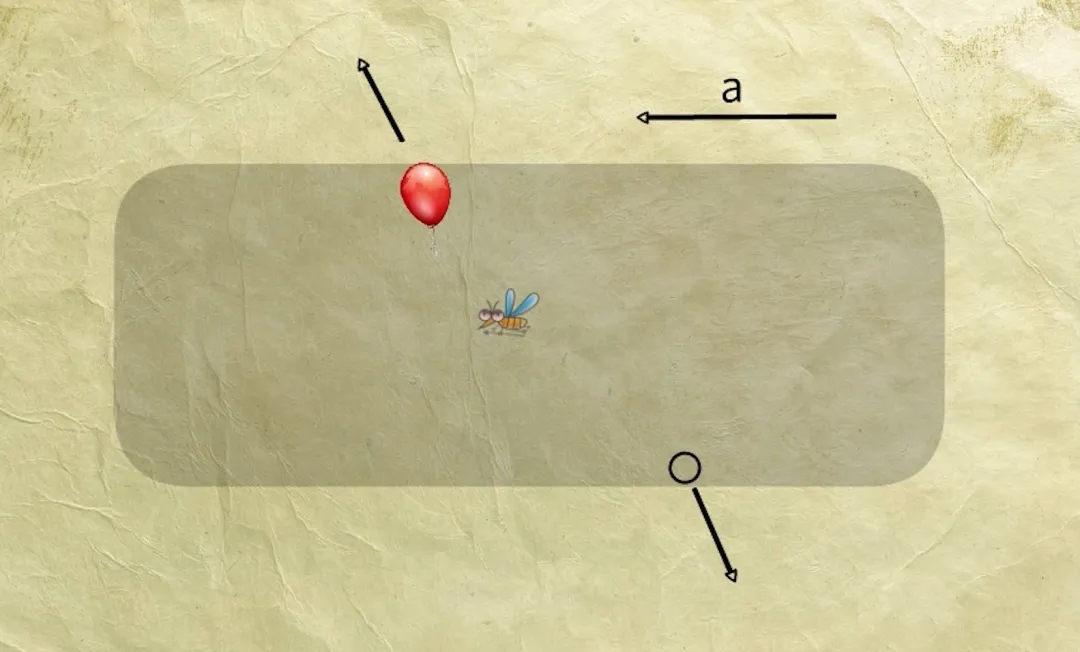
这个实验你们就不要做了,因为高铁上不允许携带氢气球……
当高铁加速时,如果我们忽略重力,仅考虑水平方向的力,蚊子的运动形态又会如何呢?

此时,蚊子运动的唯一正向力是其自身的惯性力,与之相反的是空气给予的阻力。这个问题实际上与雨滴从高空落下的问题有关。很多观众在视频评论区询问,为何雨滴从很高的地方落下不会砸伤人?
接下来,让我们来探讨一下这个问题——空气阻力与速度之间的关系。
空气阻力的计算有两种公式,一种是考虑空气粘滞力,另一种是考虑空气迎面阻力。在这两个公式中都有速度的出现,但略有差异。在第一个公式中,阻力与速度成正比;在第二个公式中,则与速度的平方成正比。
然而,两者的结论是相同的,即速度越大,阻力也会越大。
随着速度的增加,阻力最终会等于物体的重力,这时便达到了平衡状态。当阻力=重力时,物体将以恒定速度下落,此时的速度称为物体下落的最终速度。
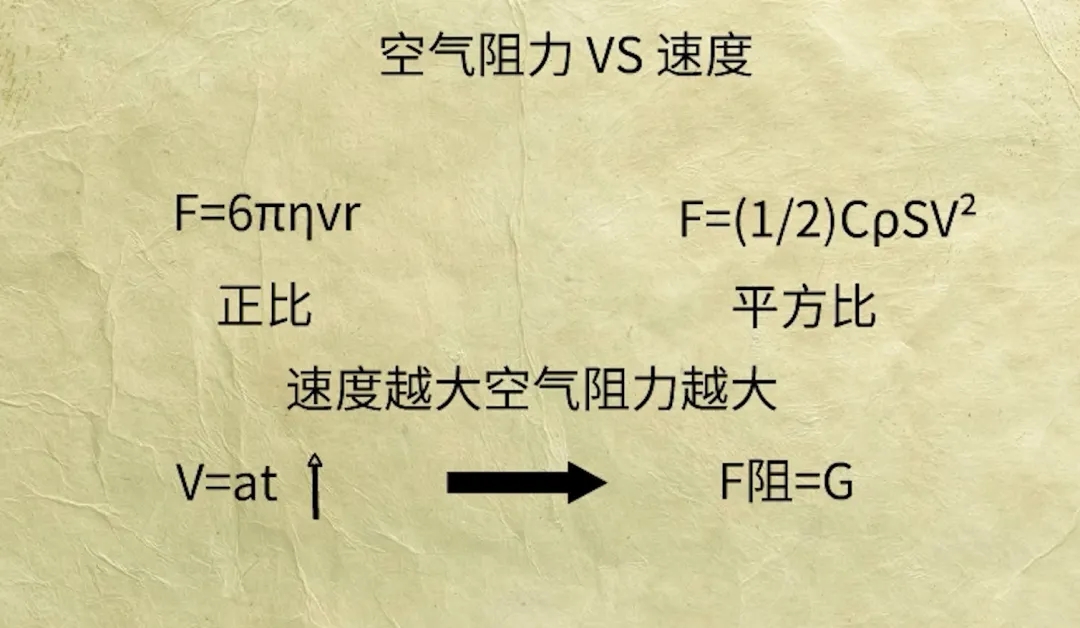
伽利略在比萨斜塔所做的实验忽略了空气阻力的因素,这个实验结果仅在真空中成立。在空气中,自由落体的物体理论上会达到恒定速度的状态,这个速度与物体的质量和表面积有关。
若有人不明白雨滴为何不会砸伤人,那是因为他们被伽利略比萨斜塔的实验误导了。关于这个实验是否真实发生过,科学界仍有争议,但无论真假,其中“相同材质但大小不同的两个球经过相同的介质,落地速度一样”的结论是不准确的。

经过计算,雨滴自由下落的最终速度大约为10m/s,相当于一辆行驶中的自行车,水滴以这个速度滴向你,并不会致死。
接下来,我们要增加难度,请大家集中注意力。
如果此时重力消失,那么雨滴会呈现何种运动形态?
暂停5秒,把你的答案打在评论区,时间不够可以自行暂停,顺便关注并长按点赞。
好,时间到,答案先不公布,我们一起走一遍流程。
此时作用在雨滴上的力还有什么?除了由运动产生的空气阻力外,几乎再无其他力。雨滴现在处于不受正向力的状态,根据前面的空气阻力公式,速度越大,空气阻力越大。在此情况下,雨滴不再受到任何正向力,唯一的外力是空气阻力,阻力会使速度减小,而速度越小,阻力也相应减小。

这里出现了一个变量,需要用到高等数学的微积分来计算。
用初中的数学知识如何理解呢?
初中数学已经学过函数,那么应该可以理解函数调用,只不过这里的调用更复杂,是互相调用。也就是说,速度和阻力是两个互相影响的函数,它们一边互相影响一边减小。
所以最后的结论,雨滴会静止吗?
从计算角度严格来说——不会。
这就涉及到一个概念——极限,这是高中数学的一个知识点。
用一个古老的数学极限问题来解释这个问题——“一尺之锤,日取其半,永世不竭”。这句话意味着,一尺长的棍子,每天砍掉它的一半,那么它永远都不会被砍完。剩余的棍子会越来越接近零,但理论上永远不会等于零。
这就是极限概念中的——无穷小。
雨滴的情况就是这样一个状态,因为不再受到额外的动力,空气阻力不断减弱了它的下坠速度。速度每降低一次,阻力就会相应减小一点,对于速度的减缓作用也随之减少,这样反复循环,理论上的速度最终将稳定在零值。
然而,如果我们要将这个无限趋近于零的速度视为静止,那么雨滴最终会停止运动。
可能你现在会问,我们不是在讨论蚊子吗?怎么会扯到雨滴去了?不过,在消失的重力作用下讨论雨滴,究竟有何意义?这种状况似乎不太可能出现。
不,其实这样的情况是有可能的,例如当高速列车从加速转为匀速行驶的状态就与此类似。
回到我们当前的场景——高速列车正在加速。回想一下我们之前讨论的蚊子状态,当时我们让它在空中悬停,让它失去了飞行能力,并且不考虑重力的作用。这时的蚊子,在列车加速过程中,就如同一个横放的雨滴在降落,只是蚊子是在一个相当于1/50的重力加速度下做自由落体运动,它会达到一个微小的终极速度,大概在5-8毫米/秒之间,这个数值存在一定的误差,因为计算中涉及的表面积和阻力系数可能存在偏差。
如果这时列车突然停止加速,进入匀速直线运动,那么蚊子由于惯性力消失,将仅受到空气阻力的影响,开始与前面提到的雨滴一样,只受阻力作用。
相较于雨滴,蚊子会更快地趋于静止状态。想象一下,如果你同时平行射出一滴水和抛出一只蚊子,水滴可能会划出半个抛物线落下,而蚊子却会在离开手之后迅速垂直下落,轨迹更像一根直立的拐杖。这主要是因为蚊子的质量更轻,且迎风面积更大。想象一下如果是柳絮,你甚至可能觉得它一离开手就停止了平行移动。
因此,如果高速列车持续加速且不考虑重力,而蚊子不飞行的话,它一定会撞上列车的尾部。但如果列车停止加速,蚊子也会随即停止向后移动。
难道我们就此打住?不妨让我们来计算一下,如何才能让列车中的蚊子一定撞上车尾。
假设列车总长200米,加速度为0.2米/秒²,一只悬停的蚊子(可以想象在无摩擦力的平面上),要让它撞到车尾,需要加速多久?在加速过程中,蚊子与列车的最终相对速度,我们取8毫米/秒,以这个速度从车头走到车尾,需要大约25000秒,即将近7小时。也就是说,只要列车保持这个加速度,经过7小时,无论蚊子在列车何处,都会撞向车尾。
在现实情况下,这个例子可以类比为,此时列车车厢末端将聚集所有的灰尘,听起来是不是有些令人惊奇?那么这种惊奇的情况真的会发生吗?
放心,不会的。那为什么不会呢?
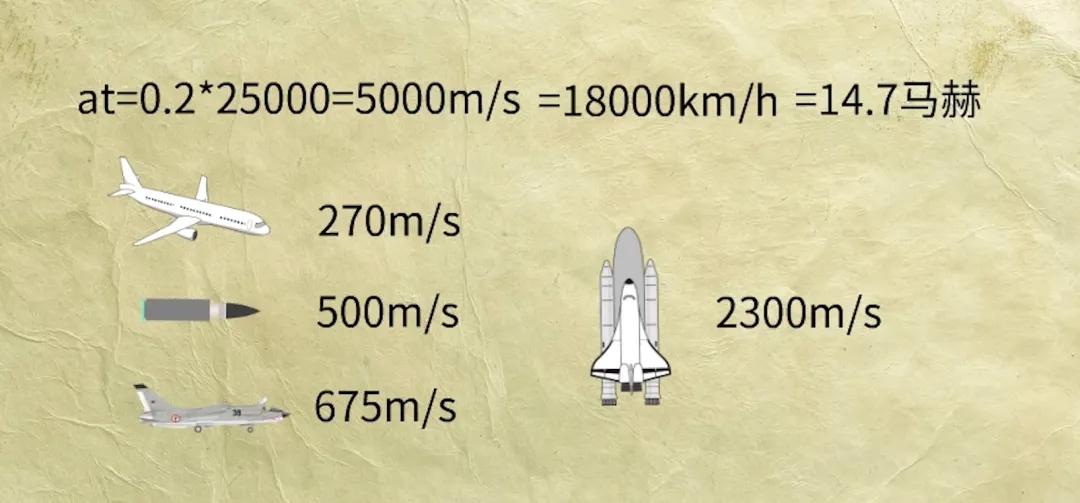
如果我们让高铁以0.2m/s²的加速度运行7小时,其速度将达到5000米/秒,18000公里/小时,14.7马赫,也就是14.7倍音速。这个速度远超大气层内所有制造物的速度极限。
我们可以对比一下其他一些看似速度很快的物体,它们的速度有多大。
民航飞机:270米/秒
子弹:500米/秒
战斗机:675米/秒
唯一能与此速度相近的是火箭助推器,速度约为2300米/秒,但仍未达到这个速度的一半。
有人可能会提到导弹,某某型号的导弹据说能达到20马赫以上。
但那是弹道导弹,它需要飞出大气层以达到这样的速度。在大气层内,火箭助推器的速度——大气层内的速度,与我们之前的例子是一致的。当进入大气层之外,它们才能进一步加速。
而普通巡航导弹的最高速度通常只有4马赫,有的甚至以亚音速飞行。
所以,我们之前提到的场景在现实中是不可能发生的。
那么在现实中,如果高铁只加速400秒然后匀速行驶,蚊子会撞到车尾吗?
最终你会发现,这实际上是一个概率问题。
在这400秒的时间里,蚊子会向车尾移动3.2米。如果蚊子可能出现在列车的任何位置,那么在行驶过程中,它有1.6%的概率会撞到车尾。
好了,我想我已经尽我所能从所有可能的角度解释了这个问题。
不知道你是否已经感受到了其中的乐趣,科学的美妙之处就在于它可以让我们从各个角度剖析任何问题。
