2024-12-18：正方形中的最多点数。用go语言，给定一个二维数组 points 和一个字符串 s，其中 points[i] 表示第 i 个点的坐标，s[i] 表示第 i 个点的标签。

如果一个正方形的中心在 （0, 0），边与坐标轴平行，并且内部没有标签相同的两个点，则称这个正方形为“合法”的。

你的任务是返回可以被“合法”正方形所包含的最多点数。

注意：

1.如果一个点位于正方形的边上或其内部，则视为在正方形内。

2.正方形的边长可以为零。

1 <= s.length, points.length <= 100000。

points[i].length == 2。

-1000000000 <= points[i][0], points[i][1] <= 1000000000。

s.length == points.length。

points 中的点坐标互不相同。

s 只包含小写英文字母。

答案2024-12-18：

chatgpt[1]

题目来自leetcode3143。

大体步骤如下：

1.创建一个 map 来存储每个标签对应的可能存在的最短距离。

2.遍历给定的每个点和其对应的标签：

• 计算这个点到 (0, 0) 的距离。• 检查是否存在其他标签对应的最短距离小于当前点到 (0, 0) 的距离，并将可能的最短距离更新到 map 中。

3.统计每个标签对应的最短距离，并最终找到可以被“合法”正方形所包含的最多点数。

时间复杂度：假设有 n 个点，则遍历所有点需要 O(n) 的时间复杂度，因此总体时间复杂度是 O(n)。

空间复杂度：使用了一个 map 存储每个标签的最短距离，以及两个长度为 26 的数组来存储最短距离，因此额外空间复杂度为 O(1)。

Go完整代码如下：package mainimport ( "fmt")func maxPointsInsideSquare(points [][]int, s string) int { min1 := make([]int, 26) for i := range min1 { min1[i] = 1000000001 } min2 := 1000000001 for i, ch := range s { x, y := points[i][0], points[i][1] j := int(ch - 'a') d := max(abs(x), abs(y)) if d < min1[j] { min2 = min(min2, min1[j]) min1[j] = d } else if d < min2 { min2 = d } } res := 0 for _, d := range min1 { if d < min2 { res++ } } return res}func abs(a int) int { if a > 0 { return a } return -a}func main() { points := [][]int{{2, 2}, {-1, -2}, {-4, 4}, {-3, 1}, {3, -3}} s := "abdca" fmt.Println(maxPointsInsideSquare(points, s))}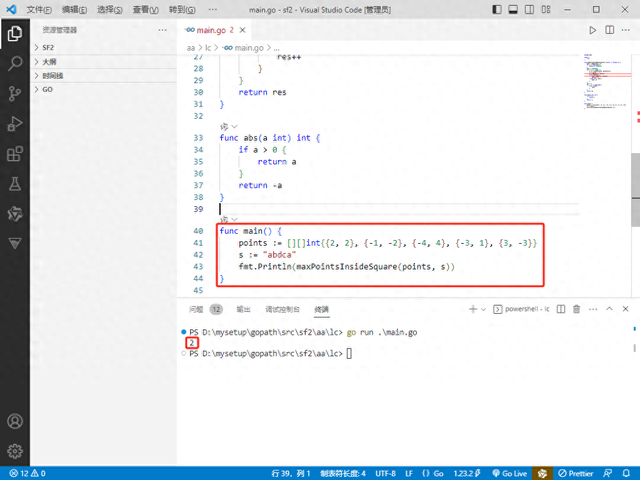

Rust完整代码如下：fn max_points_inside_square(points: Vec<Vec<i32>>, s: &str) -> i32 { let mut min1: Vec<i32> = vec![1000000001; 26]; let mut min2 = 1000000001; for (i, ch) in s.chars().enumerate() { let (x, y) = (points[i][0], points[i][1]); let j = (ch as u8 - b'a') as usize; let d = max(x.abs(), y.abs()); if d < min1[j] { min2 = min2.min(min1[j]); min1[j] = d; } else if d < min2 { min2 = d; } } let mut res = 0; for &d in &min1 { if d < min2 { res += 1; } } res}fn max(a: i32, b: i32) -> i32 { if a > b { a } else { b }}fn main() { let points = vec![vec![2, 2], vec![-1, -2], vec![-4, 4], vec![-3, 1], vec![3, -3]]; let s = "abdca"; println!("{}", max_points_inside_square(points, s));}

引用链接

[1] chatgpt: https://chatbotsplace.com/?rc=nnNWSCJ7EP