各位朋友，大家好！“数学视窗”这次给大家分享的是一道初中数学思考题，这是有关求图形中三角形面积的问题，对很多学生来说，此题难度还是比较大的，主要是难以找出解题的突破口！下面，我们就一起来看这道例题吧！

例题：（初中数学思考题）如图，已知正方形ABCD的面积是12平方厘米，正三角形△BPC的面积是3√3平方厘米，求阴影△BPD的面积是多少平方厘米？

分析：此题是已知正方形ABCD和正三角形△BPC的面积，求阴影△BPD的面积。很显然，虽然阴影△BPD的一条边BP可以费力地求出来，但是求出其面积仍然还差条件，很难求出对应的高。

那么，我们能否构造新三角形，通过面积之间的等量关系进行转化呢？由于给出的是正方形ABCD和正三角形BPC，所以由很多性质可以利用。

不妨连接AC，交BD于点O，连接PO，由已知条件可以推出PO∥DC，，所以可以得到S△POC=S△POD，故可得出S阴影=S△BPC-S△BOC。这样一来，问题即可得到解决。

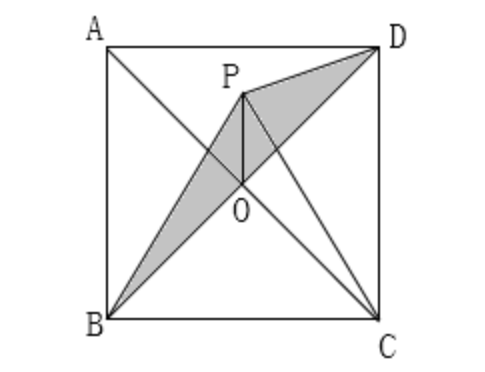
解法：如图，连接AC，交BD于点O，连接PO，

因为正方形ABCD的面积是12平方厘米，

所以S△BOC=1/4 S正方形ABCD

=1/4×12

=3（平方厘米）

根据正方形和正三角形的对称性，

（或者作垂线，证明两线重合）

所以PO∥DC，

所以S△POC=S△POD（等底等高）

则S阴影=S△BPC-S△BOC

=3√3 -3（平方厘米），

故阴影△BPD的面积是3√3 -3平方厘米.

（完毕）

这道题主要考查了正方形和正三角形性质的综合应用，以及构造图形进行面积转化问题，关键是得出两直线平行。温馨提示：朋友们如果有不明白之处或者有更好的解题方法，欢迎大家给“数学视窗”留言或者参与讨论。