2025-03-03：切蛋糕的最小总开销Ⅱ。用go语言，你有一个大小为 m x n 的矩形蛋糕，需要将其切割成 1 x 1 的小块。给定两个整数 m 和 n 以及两个数组：

1.horizontalCut：长度为 m - 1，表示在每个水平切割线 i 切割蛋糕的成本。

2.verticalCut：长度为 n - 1，表示在每个垂直切割线 j 切割蛋糕的成本。

在每次操作中，你可以选择一块不是 1 x 1 大小的蛋糕，并执行下列操作之一：

1.沿着某个水平切割线 i 切割，费用为 horizontalCut[i]。

2.沿着某个垂直切割线 j 切割，费用为 verticalCut[j]。

每次操作都会将蛋糕切割成两个独立的小部分，而每个切割的费用是固定的，不会改变。请你返回将蛋糕完全切分为 1 x 1 小块的最小总开销。

1 <= m, n <= 100000。

horizontalCut.length == m - 1。

verticalCut.length == n - 1。

1 <= horizontalCut[i], verticalCut[i] <= 1000。

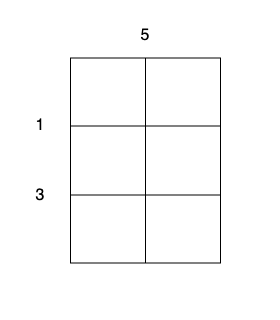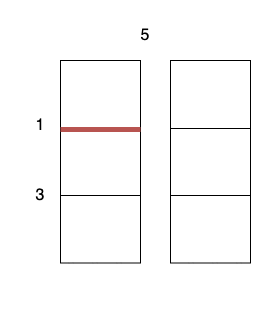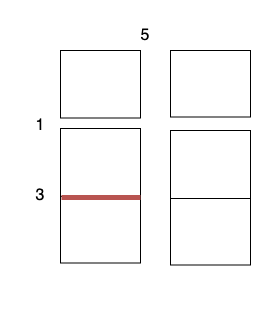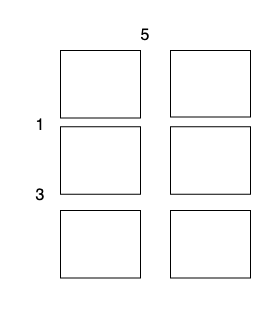
输入：m = 3, n = 2, horizontalCut = [1,3], verticalCut = [5]。

输出：13。

解释：

沿着垂直线 0 切开蛋糕，开销为 5 。

沿着水平线 0 切开 3 x 1 的蛋糕块，开销为 1 。

沿着水平线 0 切开 3 x 1 的蛋糕块，开销为 1 。

沿着水平线 1 切开 2 x 1 的蛋糕块，开销为 3 。

沿着水平线 1 切开 2 x 1 的蛋糕块，开销为 3 。

总开销为 5 + 1 + 1 + 3 + 3 = 13 。

在这里插入图片描述

答案2025-03-03：

chatgpt[1]

题目来自leetcode3219。

大体步骤如下：

1.首先，对水平切割线和垂直切割线进行排序，确保每次选择最大的切割成本。

2.初始化水平切割线和垂直切割线的数量，分别为 h = 1 和 v = 1，初始总开销 res = 0。

3.当水平切割线数组或垂直切割线数组中还有元素时，执行以下操作：

3.1.如果垂直切割线数组为空，或者水平切割线数组中最大的元素花费比垂直切割线数组中最大的元素花费大：

3.1.1.将水平切割线数组中的最大元素乘以当前的水平切割线数量 h，加到总开销 res 中。

3.1.2.将水平切割线数组中的最大元素弹出。

3.1.3.增加垂直切割线数量 v。

3.2.否则：

3.2.1.将垂直切割线数组中的最大元素乘以当前的垂直切割线数量 v，加到总开销 res 中。

3.2.2.将垂直切割线数组中的最大元素弹出。

3.2.3.增加水平切割线数量 h。

4.返回最终的总开销 res。

时间复杂度分析：

• 对水平切割线和垂直切割线进行排序的时间复杂度为 O((m-1)log(m-1) + (n-1)log(n-1))。• 进行贪心算法的过程涉及遍历水平切割线数组和垂直切割线数组，时间复杂度为 O(m + n)。• 因此，总的时间复杂度为 O((m-1)log(m-1) + (n-1)log(n-1) + m + n)。

空间复杂度分析：

• 算法过程中只使用了很少的额外空间，主要是一些变量的存储，空间复杂度为 O(1)。

所以，总的时间复杂度为 O((m-1)log(m-1) + (n-1)log(n-1) + m + n)，额外空间复杂度为 O(1)。

Go完整代码如下：package mainimport ( "fmt" "sort")func minimumCost(m int, n int, horizontalCut []int, verticalCut []int) int64 { sort.Ints(horizontalCut) sort.Ints(verticalCut) h, v := 1, 1 var res int64 for len(horizontalCut) > 0 || len(verticalCut) > 0 { if len(verticalCut) == 0 || len(horizontalCut) > 0 && horizontalCut[len(horizontalCut)-1] > verticalCut[len(verticalCut)-1] { res += int64(horizontalCut[len(horizontalCut)-1] * h) horizontalCut = horizontalCut[:len(horizontalCut)-1] v++ } else { res += int64(verticalCut[len(verticalCut)-1] * v) verticalCut = verticalCut[:len(verticalCut)-1] h++ } } return res}func main() { m := 3 n := 2 horizontalCut := []int{1, 3} verticalCut := []int{5} result := minimumCost(m, n, horizontalCut, verticalCut) fmt.Println(result)}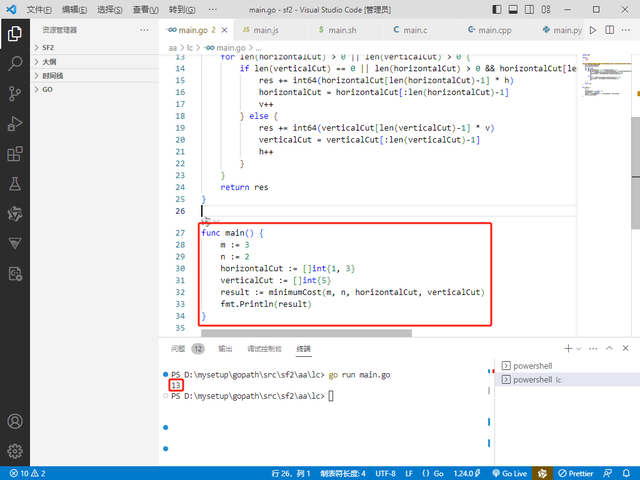

在这里插入图片描述

Python完整代码如下：

# -*-coding:utf-8-*-def minimum_cost(m, n, horizontal_cut, vertical_cut): horizontal_cut.sort() vertical_cut.sort() h, v = 1, 1 res = 0 while horizontal_cut or vertical_cut: if not vertical_cut or (horizontal_cut and horizontal_cut[-1] > vertical_cut[-1]): res += horizontal_cut[-1] * h horizontal_cut.pop() v += 1 else: res += vertical_cut[-1] * v vertical_cut.pop() h += 1 return resif __name__ == '__main__': m = 3 n = 2 horizontal_cut = [1, 3] vertical_cut = [5] result = minimum_cost(m, n, horizontal_cut, vertical_cut) print(result)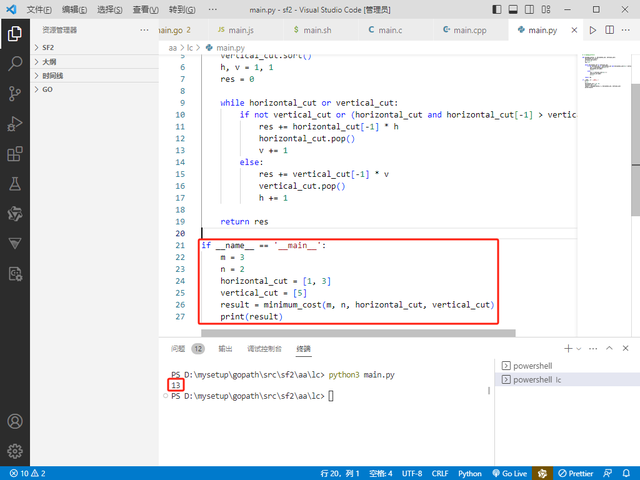

在这里插入图片描述

引用链接

[1] chatgpt: https://chatbotsplace.com/?rc=nnNWSCJ7EP