很多孩子“望题却步”、直接放弃作答,还有不少孩子完全“摸不到头脑”、束手无策!这是一道初中数学竞赛题:求非特殊角的正弦值!如图一,

图一
在直角三角形ABC中,∠ACB=18°,求sin∠ACB。
注:初中没学正弦函数与余弦函数的和差化积公式,即便通过倍数关系、将非特殊角转化成特殊角,最终还是也无法利用“特殊角的正弦值和余弦值”来求非特殊角的正弦值!
此题主要考查:①三角形相似②角平分线定理③正弦的定义④一元二次方程求根公式!
解析一:三角形相似!
①令AC=1,AB=a,由正弦定理即知sin18°=a。
②将△ABC沿BC翻折,翻折后的三角形记为△DBC,则△CAD为等腰三角形,顶角ACD=36°,AD=2a。如图二

图二
③过点D作一等腰三角形ADE即AD=DE,如图三
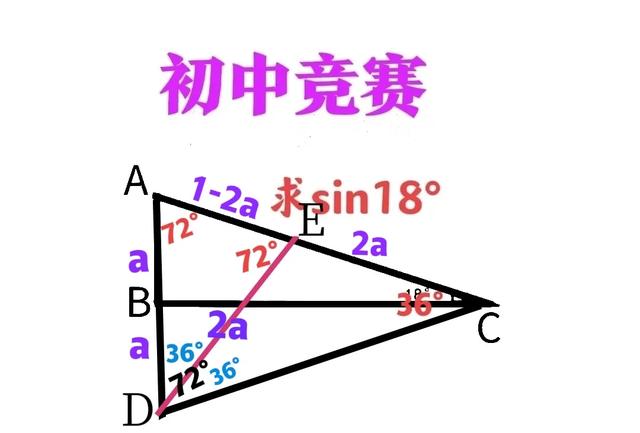
图三
④显然,∠DEA=∠DAE=72°,故∠ADE=∠EDA=36°。因此△CDE也为等腰三角形,且CE=DE=AD=2a,进而AE=AC-CE=1-2a。
⑤显然,△ACD与△ADE相似,故AC/AD=AD/AE,也即4a²=1-2a。由一元二次方程求根公式,可得a=(√2-1)/4或(-√2-1)/4,后者舍弃。因此sin18°=(√2-1)/4。
解析二:角平分线定理!
步骤①②④同于解析一。
③'过点D作∠ADC的角平分线DE,与AC相交于点E,如图三。
⑤'由角平分线定理,可得AD/CD=AE/CE,也即4a²=1-2a。同于解析一步骤⑤可得sin18°=(√2-1)/4。
————————————————
友友们有好的思路或方法,欢迎留言分享!

答案都错了!!!!!
检查一下,方程解错了。√5不是√2